| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |
Unter den Zahlensystemen nehmen die
"polyadischen" Systeme (auch B-adische Systeme genannt)
eine herausragende Stellung ein. Kennzeichnend für diese
Zahlenssysteme ist das sehr einfache Bildungsgesetz (siehe Kap.
1), das Gl. 8.1 in Form einer Potenzreihe realisiert:
Eine natürliche Zahl n wird demnach durch folgende Summe von Potenzen dargestellt:
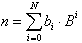 | , | (8.2) |
wobei gilt:
| B ist die Basis des Zahlensystems: | 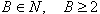
| |
| und: | ||
| bi sind Zahlenkoeffizienten: |  . . |
Die in Gl. 8.2 definierte Zahl
n wird normalerweise in einer Kurzform dargestellt, die nur die
signifikanten Koeffizienten wiedergibt. Im Zweifelsfall wird auch
die Basis B als Index angegeben:
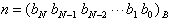 | . | (8.3) |
In dieser systemunabhängigen
Ziffernschreibweise, in der ja auch unsere Dezimalzahlen niedergeschrieben
werden, können am Anfang stehende Nullen unterdrückt
werden. Bei bestimmten arithmetischen Operationen sind aber auch
diese führenden Nullen zu berücksichtigen, um leicht
auftretende Fehler zu vermeiden (s.u.).
In Kap. 1.1 wurden bereits die wichtigsten
polyadischen Zahlensysteme unterschieden, die den Basiswerten
2, 8, 10 und 16 entsprechen:
| Dualsystem | |
| Oktalsystem | |
| Dezimalsystem | |
| Hexadezimalsystem |
Tab. 8.1: Wichtige polyadische Zahlensysteme
Das oben erwähnte sumerisch-babylonische
Zahlensystem (Basis 60) wird als "sexagesimales" Zahlensystem
bezeichnet.
Gleichungen 8.2-3 zeigen, daß
die Position eines Koeffizienten einer genau bestimmten Wertigkeit
entspricht (einem Gewicht). Dies ist äquivalent mit der oben
wiedergegebenen Definition für ein positionelles Zahlensystem.
Entsprechend Gl. 8.2 können auch Brüche dargestellt werden, indem man negative Werte für den Index bzw. den Exponenten i zuläßt:
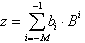 | . | (8.4) |
Faßt man schließlich
Gl. 8.2 und 8.4 zusammen, ergibt sich die Beschreibung der reellen
Zahlen:
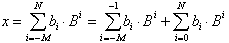 | . | (8.5) |
Oder in Ziffernschreibweise:
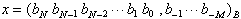 | . | (8.6) |
Aus Gl. 8.2 läßt sich durch schrittweises Ausklammern der Basis B eine weitere Darstellungsform gewinnen, die auf Grund ihrer algorithmischen Anwendungsmöglichkeiten von großer Bedeutung ist:
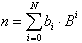 |
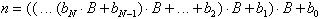 | . | (8.7) |
Dieses in Gl. 8.7 definierte Verfahren
ist in der Mathematik als das Horner-Schema bekannt.
Auch der durch Gl. 8.4 beschriebene
gebrochene Anteil kann über das Horner-Schema beschrieben
werden:
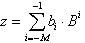 |
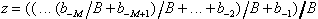 | . | (8.8) |
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |