| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |
Da numerische Information in unterschiedlichen
Zahlensystemen dargestellt werden kann, besteht die Notwendigkeit,
Umwandlungen (Konvertierungen) zwischen diesen Systemen durchzuführen.
Insbesondere zwei Methoden für
diese Zahlenkonvertierung können direkt aus der zugrundeliegenden
Potenzreihendefinition Badischer Zahlen hergeleitet werden:
Bei dieser Methode wird in einfachster
Weise die Potenzreihendefinition (8.2) umgesetzt.
Beginnend mit der höchsten Potenz
(i = N) wird der maximale Koeffizient b1
bestimmt, für den gilt:
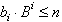 | . |
Dieser erste Koeffizient ist natürlich
immer größer als 0. Der Wert 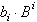 wird von der zu wandelnden Zahl subtrahiert, um daraufhin die
nächstkleinere Potenz zu ermitteln (i < N),
für die gilt:
wird von der zu wandelnden Zahl subtrahiert, um daraufhin die
nächstkleinere Potenz zu ermitteln (i < N),
für die gilt:
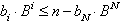 | . |
Dieser Prozeß wird wiederholt,
bis schließlich der Index i = 0 erreicht wird
und alle Koeffizienten bi
bestimmt wurden.
In dieser Konvertierungsmethode wird
also der höchstwertige Koeffizient zuerst bestimmt, die niederwertigen
Koeffizienten folgen ("Groß nach Klein").
8.3.2 Die Methode der wiederholten Multiplikation/Division
8.3.2.1 Umwandlung ganzer Zahlen
Diese algorithmisch sehr einfach aufgebaute Umwandlungsmethode folgt aus dem in Gl. 8.7 dargestellten Horner-Schema. Die Zahl n wird in einer beliebigen Basis dargestellt und soll in eine Darstellung mit Basis B konvertiert werden.
Dies bedeutet, daß die Koeffizienten b0, b1, ..., bN bestimmt werden müssen. Diese Koeffizientenbestimmung kann durch sukzessive Division der Zahl n durch die Basis B erreicht werden.
Der Vorgang benötigt N Schritte,
deren Wirkung in der folgenden Tabelle zusammengefaßt wird:
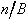 |
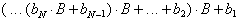 | 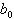 | |
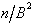 |
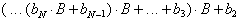 | 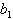 | |
|
|
|
|
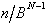 |
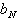 | 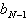 | |
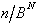 |
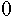 | 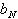 |
Tab. 8.2: Zahlenkonvertierung durch wiederholte Division.
Durch schrittweise Division von n
durch B werden die gesuchten Koeffizienten bi
also nacheinander ermittelt, wobei der Wert von b0
zuerst bestimmt wird ("Klein nach Groß").
8.3.2.2 Umwandlung reeller bzw. gebrochener Zahlen
In ähnlicher Form kann die Konvertierung
gebrochener Zahlen durchgeführt werden. Allerdings werden
in diesem Fall der Vorkommateil und der Nachkommateil der Zahl
getrennt konvertiert. Die Wandlung des Vorkommateils folgt exakt
der oben beschriebenen Regel für ganze Zahlen.
Wie das Horner-Schema Gl. 8.8 zeigt,
muß für die Umwandlung des Nachkommateils eine wiederholte
Multiplikation mit dem Basiswert vorgenommen werden.
Im Vergleich zur Wandlung einer ganzen
Zahl kommt allerdings eine weitere Komplikation hinzu:
Ganze (natürliche) Zahlen haben
eine genau vorgegebene maximale Größe. Dies bedeutet,
daß die Konvertierung immer in genau N Schritten durchgeführt
werden kann. Im Fall einer gebrochenen Zahl kann die Anzahl der
notwendigen Umwandlungsschritte nicht ohne weiteres vorhergesagt
werden. Auch wenn die umzuwandelnde Zahl einen endlichen Bruch
darstellt, wird der in die Basis B gewandelte Bruch nicht notwendigerweise
endlich bleiben.
Die Konvertierung kann in eine von
drei Klassen eingeordnet werden, denen zufolge der Ergebniswert
dargestellt wird als
Die Umwandlungsschritte der sukzessiven
Multiplikation werden in der nachfolgenden Tabelle zusammengefaßt:
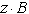 |
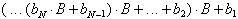 | 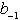 | |
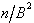 |
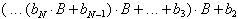 | 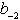 | |
|
|
|
|
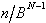 |
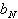 | 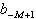 | |
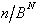 |
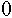 | 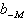 |
Tab. 8.3: Zahlenkonvertierung durch wiederholte Multiplikation.
Hinweis zum Algorithmus:
8.3.3 Umwandlung zwischen "verwandten" Zahlensystemen
Bei der Zahlenkonvertierung zwischen
zwei polyadischen Systemen muß immer gelten:
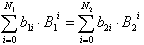 | . | (8.9) |
Die Summe zweier Zahlenpolynome bleibt
unverändert beim Übergang von einem System mit der Basis B1
zu einem System mit der Basis B2.
Die Konvertierung wird dann besonders
leicht, wenn die Basiswerte in einem einfachen Verhältnis
zueinander stehen, insbesondere wenn gilt:
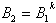 | (k ganzzahlig). | (8.10) |
Dies ist z.B. der Fall im Vergleich
des Dualsystems mit dem Oktal- und Hexadezimalsystem. (8 = 23,
16 = 24).
Für diese Systeme gilt also:
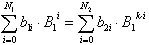 | . | (8.11) |
Wird diese Potenzreihe unterteilt
in Gruppen mit jeweils k Elementen (Produkten), ergibt sich:
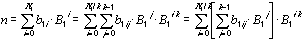 |
Diese Umwandlung in Gruppen ist natürlich
nur dann möglich, wenn N1/k
wiederum eine ganze Zahl ergibt. Die Positionszahl N1
muß also ein ganzzahliges Vielfache von k sein. In der Praxis
wird dies dadurch erreicht, daß die zu konvertierende Zahl
auf der höherwertigen Seite mit einer entsprechenden Anzahl
von Nullen aufgefüllt wird.
| Mit | 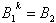 | und | |
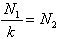
| |||
| folgt also: | |||
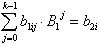
| |||
| und damit: | |||
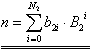 | . | (8.12) |
Liegt der hier beschriebene Fall vor, können zur Zahlenumwandlung von dem System mit Basis B1 zum System mit Basis B2 Gruppen von jeweils k Ziffern b1i zu einem neuen Koeffizienten b2j zusammengefaßt werden.
Der Zusammenfassungsprozeß
muß an der Position des Kommas (Dezimalpunktes) begonnen
werden und von dort nach links bzw. (bei Bruchzahlen) nach rechts
fortgesetzt werden.
Bei der Konvertierung von Dualzahlen
in das Hexadezimalsystem ergibt sich demzufolge:
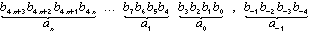 | (8.13) |
| mit: | ai | = Koeffizient im Hexadezimalsystem (B2 = 16), |
| bi | = Koeffizient im Dualsystem (B1 = 2). |
8.3.4 Zahlenkonvertierung: Beipiele
Die eingeführten Methoden sind
in aller Allgemeinheit für die Konvertierung zwischen beliebigen
Badischen Zahlensystemen einsetzbar.
Größere Bedeutung kommt
"naturgemäß" dem Dezimalsystem zu, das Dualsystem
nimmt auf Grund seiner Anwendung in technischen Systemen eine
besondere Stellung ein. Die Umwandlung zwischen diesen beiden
Systemen soll deshalb zunächst an Beispielen erläutert
werden.
Danach wird eine Ausweitung auf andere Systeme vorgenommen.
Beispiel 8.1:
Umwandlung der Zahl +39,62510
in das Dualsystem nach der "Potenz-Methode":
Rest Zweierpotenz Dezimalwert Binärwert
39,625 5 32 1
7,625 4 16 0
7,625 3 8 0
7,625 2 4 1
3,625 1 2 1
1,625 0 1 1,
0,625 -1 0,5 1
0,125 -2 0,25 0
0,125 -3 0,125 1
___________
100111,1012
Ergebnis: 39,62510 = 100111,1012
Beispiel 8.2:
Umwandlung der Zahl +39,62510
in das Dualsystem nach der "Quotient-Produkt-Methode":
In diesem Fall wird die Umwandlung in zwei Phasen aufgeteilt:
1. Konvertierung des Vorkommateils:
Division Quotient Rest
39:2 19 1
19:2 9 1
9:2 4 1
4:2 2 0
2:2 1 0
1:2 0 1
______
100111
2. Konvertierung des Nachkommateils:
Multiplikation Produkt Vorkomma Nachkomma Binärwert
0,625*2 1,25 1 0,25 ,1
0,25 *2 0,5 0 0,5 0
0,5 *2 1,0 1 0,0 1
_________
,101
Zusammenfassung beider Teilresultate ergibt wiederum:
Beispiel 8.3:
Rückwandlung der Dualzahl 100111,1012 in die entsprechende Dezimalzahl unter Benutzung der "Quotient-Produkt-Methode".
In diesem Fall muß wiederholt
durch 1010 = 10102
dividiert werden:
Division Quotient Rest
100111:1010 11 1001
11:1010 0 11
_____________
Ergebnis: (112) (10012)
dem entspricht: 3910
Die Wandlung des gebrochenen Anteils
der Dualzahl in Beispiel 8.2 kann durch fortgesetzte Multiplikation
mit 10102 erreicht werden.
Beispiel 8.4:
Wandlung der Dualzahl n = 11011011002
in die entsprechende oktale bzw. hexadezimale Repräsentation.
Diese Konvertierung ist besonders
einfach, da zunächst Dreier- bzw. Vierergruppen von Bits
gebildet werden können, die dann getrennt umgewandelt werden.
dual 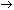 oktal: oktal: | n = | 001 | 101 | 101 | 100 |
| oktale Werte der Dreiergruppen: |
dual 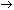 hexadezimal: hexadezimal: | n = | 0011 | 0110 | 1100 |
| hexadezimale Werte der Vierergruppen: |
Hinweis:
Im Falle der Umwandlung
in das hexadezimale System müssen die in Kap. 1 definierten
Symbole A - F verwendet werden, um die Zahlen 1010
bis 1510
darzustellen.
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |