 |
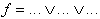 | DNF (UND/ODER-Form) |
| Umformung mit Hilfe des "de Morgan"-Theorems ergibt daraus: | ||
 | (NAND-Form) | |
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |
Elementare Beschreibungsformen
Um eine Boolesche Funktion mit Hilfe von KV-Diagrammen zu vereinfachen (minimisieren), ist eine Zusammenfassung von Feldern notwendig. Dieser Prozeß ist sowohl bei 0- als auch bei 1-Feldern anwendbar. Zur Charakterisierung der Felder können außerdem deren Argumente oder die Komplemente dieser Argumente herangezogen werden.
Es gibt also eine Vielzahl von Kombinationsmöglichkeiten,
die nachfolgend noch einmal zusammengestellt werden.
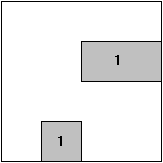
2.6.1 Zusammenfassung von 1-Feldern
Beschreibung der Booleschen Funktion über die 1-Felder:
 |
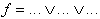 | DNF (UND/ODER-Form) |
| Umformung mit Hilfe des "de Morgan"-Theorems ergibt daraus: | ||
 | (NAND-Form) | |
Beschreibung der Booleschen Funktion über die Komplemente der 1-Felder:
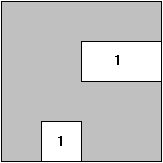 |
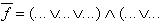 | (ODER/UND-Form) |
| Umformung mit Hilfe des "de Morgan"-Theorems ergibt daraus: | ||
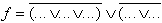 | (NOR/ODER-Form) | |
2.6.2 Zusammenfassung von 0-Feldern
Beschreibung der Booleschen Funktion über die 0-Felder:
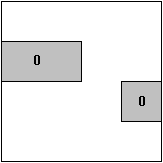 |
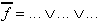 | (UND/ODER-Form) |
| Umformung mit Hilfe des "de Morgan"-Theorems ergibt daraus: | ||
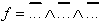 | (NAND/UND-Form) | |
Beschreibung der Booleschen Funktion über die Komplemente der 0-Felder:
 |
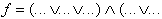 | KNF (ODER/UND-Form) |
| Umformung mit Hilfe des "de Morgan"-Theorems ergibt daraus: | ||
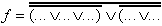 | (NOR-Form) | |
2.6.3 Umwandlung von UND/ODER-Netzen
Von den oben angegebenen zweistufigen
Netzwerkvarianten sind die UND/ODER-Form (DNF) sowie die ODER/UND-Form
(KNF) besonders wichtig, da sie anschaulich sehr einfache Beschreibungsformen
darstellen.
Definition:
Ein mehrstufiges Verknüfungsnetz mit einer beliebigen Anzahl von Ein- und Ausgängen wird als UND/ODER-Netz bezeichnet, wenn auf jedem beliebigen Signalpfad zwischen einem Eingang und einem Ausgang UND- und ODER-Funktionen abwechselnd durchlaufen werden.Beispiel:
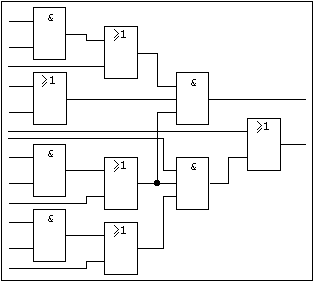
Abb. 2.29: Typisches UND-ODER-NETZ.
Praktisch bedeutender als die UND/ODER-Netze
sind allerdings die mit NAND- bzw. NOR-Gattern realisierten Schaltungen,
da diese Grundgatter technologisch günstiger zu fertigen
sind.
Die Wandlung von UND/ODER/INVERS-Schaltungen
in NAND/NOR-Schaltungen ist deshalb außerordentlich wichtig.
Diese Transformation folgt wiederum dem "De Morgan"-Theorem
und kann daher als ein einfaches dreischrittiges Verfahren formuliert
werden:
Umwandlungsbeispiele (zweistufige Netzwerke):
UND/ODER NAND:
 | (2.11) |
ODER/UND NOR:
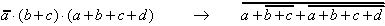 | (2.12) |
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |