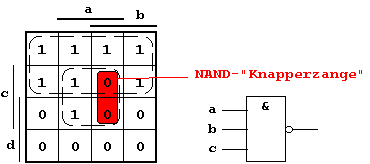
Abb. 2.30: Einsatz der NAND-"Knapperzange".
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |
Bei der Realisierung und Vereinfachung
einer Booleschen Funktion kann folgende Situation auftreten:
Beispiel:

Abb. 2.30: Einsatz der NAND-"Knapperzange".
Die im KV-Diagramm gestrichelt gezeichneten
Feldverbunde führen zu folgender DNF-Realisierung:
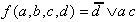 | . | (2.13) |
Offensichtlich entspricht diese BFkt nicht der vorgebenen Funktion, da im makierten Zweierverbund die notwendigen Nullen nicht erzeugt werden.
Abhilfe ist möglich durch Einsatz eines "Werkzeuges", das aus dem zu groß geratenen 1-Feldverbund die zwei fehlerhaften Einsen "herausknappert", eine "Knapperzange" also.
Dieses Werkzeug kann in einfacher
Weise durch ein NAND-Gatter implementiert werden, das für
a=b=c=1 eine '0' produziert, d.h. die beiden '1'-Werte herausschneidet.
Algebraisch gesehen ist also eine
konjunktive Verknüpfung des zu großen 1-Feldes mit
der NAND-Knapperzange notwendig, was zur gesuchten BFkt führt:
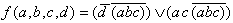 | (2.14) |
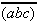 | repräsentiert
die "Knapperzange". | (2.14) |
bzw. bei NAND-Realisierung:
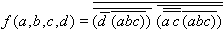 | (2.15) |
2.7.2 Vereinfachungen durch "don't care"-Fälle
Es kann der Fall eintreten, daß für eine Boolesche Funktion bei bestimmten Werten der Argumente kein eindeutiger Ergebniswert in der Spezifikation vorgesehen ist.
Dieser Fall tritt z.B. immer dann
ein, wenn auf Grund des vorgegebenen Problems der entsprechende
Wert der Argumente nicht auftreten kann. Bei der Anwendung der
Schaltung ist es also unbedeutend, ob das Verknüpfungsnetz
bei diesen Eingangswerten eine '0' oder eine '1' erzeugt. Dieser
Fall wird als "don't care" bezeichnet.
Im KV-Diagramm führt dieser
"don't care"-Fall dazu, daß an der entsprechenden
Position zunächst "willkürlich" entweder der
Wert '0' oder der Wert '1' eingesetzt werden kann. Für die
Schaltungsreduzierung bedeutet dies einen zusätzlichen Freiheitsgrad,
da der Wert des Feldes in Abhängigkeit von den Nachbarfeldern
so optimiert werden kann, daß die Bildung möglichst
großer Primimplikanden möglich wird.
Beispiel:
Die folgende Funktion sei vorgegeben:
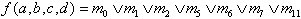 | . | (2.16) |
| Mm9 sei "don't care". |
Die Funktion wurde in diesem Beispiel
über die Minterme definiert, wobei folgende Indizierung der
KV-Diagrammfelder gilt:
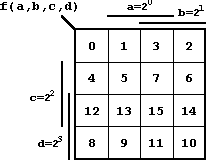
Abb. 2.31: Minterm-Indizierung bei 4 Variablen.
Damit kann das zur BFkt gehörende KV-Diagramm angegeben werden:
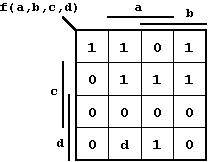
Abb. 2.32: KV-Diagramm zur Booleschen Funktion Gl. 2.16.
In diesem Beispiel ist m9 (d = '1') Partner von m1
bzw. m11;
es läßt sich ein Kern-PI aus m9
und m11
sowie ein relativ eliminierbarer PI aus m9
und m1
bilden. Die Lösung ist damit (DNF):
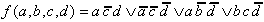 | (2.17) |
In ähnlicher Weise kann M9
(d = '0') als Partner von M8,
M12
und M13
interpretiert werden, was zur Bildung eines zusätzlichen
Kern-PI führt. Die Lösung lautet in diesem Fall (KNF):
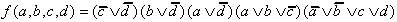 | (2.18) |
Dieses Beispiel zeigt also, wie in
einem vorgegebenen KV-Diagramm ein bestehendes "don't
care"-Feld entweder als Minterm oder als Maxterm realisiert
werden kann, um die Bildung größtmöglicher Feldverbunde
vorzubereiten.
Das "don't care"-Feld
wird natürlich nicht eingesetzt, um in einer DNF oder KNF
einen zusätzlichen Minterm bzw. Maxterm zu erzeugen.
An den beiden obigen Lösungen
kann außerdem aufgezeigt werden, wie ein weiterer, für
die Schaltungsimplementierung wichtiger Parameter durch Feldverbundbildung
minimisiert werden kann: die Anzahl der Gattereingänge c
(engl. pin count).
| kDNF (zum Vergleich) | c = 7·4 + 7 = 35 |
| DNF | c = 4·3 + 4 = 16 |
| KNF | c = 3·2 + 3 + 4 + 5 = 18 |
Bei den Verbundlösungen (DNF
bzw. KNF) wird ein "double rail"-System vorausgesetzt.
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |