2 Entwurf von Verknüpfungsnetzen

2.5 Primimplikanden

Die oben eingeführten Feldverbunde können wichtige Eigenschaften der Booleschen Funktion wiederspiegeln. Diese Eigenschaften hängen von der Größe der Feldverbunde sowie der Beziehung der Feldverbunde untereinander ab. Um deren Besonderheiten zu unterstreichen, werden unterschiedliche Formen der Verbunde differenziert, was zu den folgenden Definitionen führt:

Definition: Implikand

Als Implikand wird ein anschaulicher Feldverbund im KV-Diagramm bzw. der entsprechende algebraische Term bezeichnet. "Implikand" und "Feldverbund" sind in diesem Sinne also synonym.

Definition: Primimplikand (PI)

Ein Implikand einer Booleschen Funktion wird als Primimplikand bezeichnet, wenn er in keinem anderen Implikanden vollständig enthalten ist.

Definition: Kern-Primimplikand (KPI)

Enthält ein Primimplikand (PI) mindestens eine Vollkonjunktion, die in keinem anderen PI enthalten ist, spricht man von einem Kern-Primimplikanden (KPI).

Abb. 2.22: Definition der Implikanden.

Wie an einfachen Beispielen verifiziert werden kann, ist normalerweise die Bildung zahlreicher Implikanden, Primimplikanden bzw. Kern-Primimplikanden möglich. Es stellt sich die Frage, welche dieser Verbunde in der Schaltungsrealisierung unbedingt Verwendung finden müssen.

Regel:

Kern-Primimplikanden müssen in einer Schaltungsrealisierung grundsätzlich berücksichtigt werden! Sie bilden also den "Kern" der Schaltung.
Primimplikanden können oftmals von einer Realisierung eliminiert werden, allerdings hängt ihre Eliminierbarkeit von weiteren Eigenschaften ab.

Dies führt zu zwei weiteren Begriffsdefinitionen:

Definition: Absolut eliminierbarer Primimplikand

Ein PI ist absolut eliminierbar, wenn es für die gegebene Bfkt eine Disjunktion von Kern-PIs gibt, die ihn vollständig enthält.

Definition: Relativ eliminierbarer Primimplikand

Ein PI ist relativ eliminierbar, wenn er weder einen KPI darstellt noch absolut eliminierbar ist. Ein Teil dieser relativ eliminierbaren PIs muß in der Schaltungsrealisierung verwendet werden.

Bei der Suche nach einer minimalen Form einer BFkt (dies sei zunächst eine Form mit möglichst wenigen Gattereingängen) kann also folgende Klasseneinteilung bzw. Rangfolge bei der Implikandenberücksichtigung vorgenommen werden:

Kern-PIs:
Sie müssen in der Schaltungsrealisierung unbedingt berücksichtigt werden;
relativ eliminierbare PIs:
Nur eine Teilmenge muß berücksichtigt werden;
absolut eliminierbare PIs:
Die Berücksichtigung dieser PIs ist nicht notwendig.

Beispiel: Klassifizierung von Implikanden:

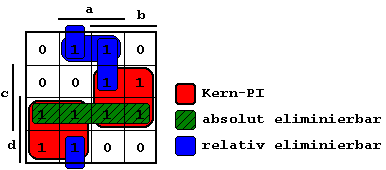
Abb. 2.23: KV-Diagramm mit klassifizierten Implikanden.

Für die Beschreibung der Booleschen Funktion lassen sich zwei minimale Formen wählen, die sich nur durch Auswahl der relativ eliminierbaren PIs unterscheiden:

oder

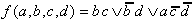Hinweis:

Sämtliche für 1-Feldverbunde formulierte Regeln gelten in äquivalenter Form auch für 0-Feldverbunde.

2.5.1 Quine-McCluskey-Verfahren

Außer dem hier eingeführten grafischen Weg zum Auffinden der Primimplikanden existieren auch algorithmische Lösungsmethoden. Das wohl bekannteste Verfahren geht auf Quine und McCluskey zurück.

Das nach ihnen benannte Minimierungsverfahren kann mit dem KV-Diagramm-Verfahren verglichen werden, da beide Methoden auf die gleichen algebraischen Prinzipien zurückgehen.

Die Karnaugh-Veitch-Methode hat allerdings den Nachteil, daß auf Grund der grafischen Methodik eine Begrenzung auf fünf bis sechs Argumente sinnvoll ist. Außerdem ist bei mehreren ähnlichen minimalen Formen eine direkte Ausgabe über die absolut minimale (also optimale) Realisierung nicht möglich.

Das Quine-McCluskey-Verfahren geht in ganz ähnlicher Form vor, benutzt aber einen exakt definierbaren tabellarischen Vorgang, um die Primterme der Booleschen Funktion zu bestimmen. Dieser erste Teilschritt geht auf Quine zurück.

Eine ebenfalls tabellarische Erweiterung wurde später von McCluskey beschrieben, um aus diesen Primtermen, diejenigen auszuwählen, die für eine minimale Realisierung berücksichtigt werden müssen.

2.5.1.1 Quine-Verfahren

Dieses Verfahren beruht wie die KV-Methode auf der Beziehung

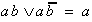(2.7)

aus der ebenfalls die Nachbarschaftsbeziehung und die daraus resultierende Vereinfachungsmöglichkeit im KV-Diagramm abgeleitet wurde.

Das Quine-Verfahren geht zunächst von einer kanonischen Normalform der Booleschen Funktion aus, z.B. einer kDNF. Sämtliche Vollkonjunktionen dieser kDNF werden dann in einer Tabelle geordnet, wobei zunächst eine Gruppierung nach der Anzahl der vorhandenen Einsen vorgenommen wird (d.h. der nichtinvertierten Argumente); innerhalb der einzelen Gruppen wird außerdem noch nach Wertigkeit geordnet.

Dieser erste Schritt soll zunächst am Beispiel der oben durch ein KV-Diagramm definierten Bfkt. detailliert werden.

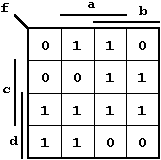
Abb. 2.24: KV-Diagramm der Beispielfunktion.

Die durch ihre Argumente "dcba" beschrieben Vollkonjunktionen

1000, 1100, 1110, 0110, 0011,
1011, 1111, 0111, 0001, 1001.

werden nun tabellarisch zusammengestellt und nach Anzahl der vorhandenen Einsen gruppiert:

Gruppe	Vollkonjunktion		Status
	dcba	Wert
0	nicht vorhanden
1	0001	1
	1000	8
2	0011	3
	0110	6
	1001	9
	1100	12
3	0111	7
	1101	13
	1110	14
4	1111	15

Tab. 2.1: Gruppierte Tabelle der Vollkonjunktionen.

Um Gl. (2.7) anwenden zu können, müssen paarweise diejenigen Vollkonjunktionen herausgefunden werden, die sich nur in einem Argument unterscheiden. Das bedeutet, daß in Tab. 2.1 nur Vollkonjuktionen benachbarter Gruppen verglichen werden müssen.

In Paaren, die diese Bedingung erfüllen, kann das unterschiedliche Argument eliminiert werden.

Diese "Kürzung" wird in Tab. 2.1 markiert (hier z.B. durch Häkchen) und in einer zweiten Tabelle durch einen Strich an der Stelle des eliminierten Argumentes vorgenommen.

Gruppe	dcba	dezimal	Status
1-2	00-1	1- 3
1-2	-001	1- 9
1-2	100-	8- 9
1-2	1-00	8-12
2-3	0-11	3- 7
2-3	011-	6- 7
2-3	-110	6-14
2-3	1-01	9-13
2-3	110-	12-13
2-3	11-0	12-14
3-4	-111	7-15
3-4	11-1	13-15
3-4	111-	14-15

Tab. 2.2: Gruppierte Tabelle nach 1. Kürzung.

Dieser Prozeß wird wiederholt, solange Kürzungen durchgeführt werden können. Als nächstfolgende Tabelle ergibt sich in diesem Beispiel:

Gruppe	dcba	dezimal	Status
1-2,2-3	1-0-	8- 9,12-13
1-2,2-3	1-0-	8-12, 9-13
2-3,3-4	-11-	6- 7,14-15
2-3,3-4	-11-	6-14, 7-15
2-3,3-4	11--	12-13,14-15
2-3,3-4	11--	12-14,13-15

Tab. 2.3: Gruppierte Tabelle nach 2. Kürzung.

Wie aus Tab. 2.3 ersichtlich, ist in diesem Fall eine weitere Kürzung nicht möglich. Der von Quine angegebene tabellarische Prozeß ist damit abgeschlossen.

Die in den Kürzungstabellen nicht abgehakten Terme sind die gesuchten Primimplikanden der gegebenen Booleschen Funktion:

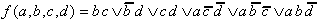Offensichtlich handelt es sich hierbei um alle bestehenden Primimplikanden, also auch um diejenigen, die zur Funktionsrealisierung nicht notwendig sind.

An dieser Stelle greift der von McCluskey entwickelte Selektionsprozeß ein.

2.5.1.2 McCluskey-Verfahren

Auch dieses Verfahren ist tabellarisch organisiert. Zur Auswahl der notwendigen Implikanden werden alle Vollkonjunktionen (Minterme) in einer Tabelle den gefundenen Primimplikanden gegenübergestellt.

	Primimplikanden
Minterm
m₀
m₁				x	x
m₂
m₃				x		x
m₄
m₅
m₆	x
m₇	x					x
m₈		x
m₉		x			x
m₁₀
m₁₁
m₁₂		x	x
m₁₃		x	x
m₁₄	x		x
m₁₅	x		x

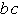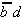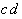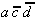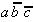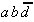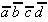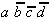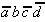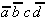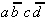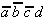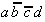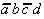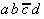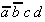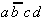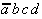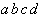Tab. 2.4: Auswahltabelle nach McCluskey
(dunkle (rote) Zellen markieren KPI-Spalten).

In dieser Tabelle können zunächst die Vollkonjunktionen bestimmt werden, die nur in einem Primimplikanden auftreten. Die so ausgezeichneten Primimplikanden sind demzufolge Kernprimimplikanden, die unbedingt verwendet werden müssen.

Zur weiteren Verarbeitung können aus Tab. 2.4 die (als notwendig erkannten) KPIs gelöscht werden, die entsprechenden Spalten und die Zeilen mit bereits realisierten Mintermen können eliminiert werden.

Die so entstehende reduzierte Tabelle (Tab. 2.5) zeigt:

Der Primimplikand ist redundant und damit absolut-eliminierbar (alle Minterme wurden bereits realisiert).

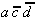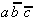, und sind relativ-eliminierbar; es muß entweder nur 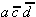realisiert werden oder aber gemeinsam mit .

Primimplikanden

Minterm

m₀

m₁ x x

m₂

m₃ x x

m₄

m₅

m₁₀

m₁₁

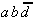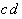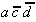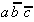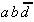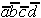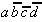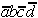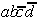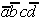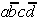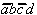Tab. 2.5: Reduzierte Auswahltabelle nach McCluskey.

Um eine minimale Bfkt. zu erhalten, sollten möglichst wenige gleichwertige Primimplikanden genutzt werden. Mit dieser Vorgabe kann aus Tab. 2.5 eine weitere Reduktion abgeleitet werden. Zur Realisierung der Minterme m₁ und m₃ reicht es, den Primimplikanden 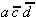zu berücksichtigen.

Für die entgültige minimale (optimale) Boolesche Funktion ergibt sich damit:

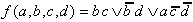Dieses Ergebnis stimmt mit dem bereits vorher erzielten überein.

Hinweis:

Das mit dem Quine-McCluskey-Verfahren gefundene Ergebnis stellt eine minimale Boolesche Funktion dar. Auch hierbei kann es natürlich mehrere äquivalente minimale Lösungen geben.

Die Lösungsfunktion liegt als DNF vor, die mit Hilfe des "De Morgan"-Theorems in die gewünschte Realisierungsform umgewandelt werden kann (NAND-, NOR-Struktur, etc.).

Der Vorteil des Quine-McCluskey-Verfahrens liegt in dem genau definierten Algorithmus zur Auffindung der Lösungsfunktionen. Damit eröffnet sich der Weg zu einer einfachen z.B. programmierten Lösungsmethode.

Ein wesentlicher Nachteil des Verfahrens ist, daß die zu minimierende Funktion immer als kanonische Normalform vorliegen muß (kDNF oder kKNF). Unter Umständen muß also eine Erweiterung der Funktion vorgenommen werden. Dies bedeutet außerdem, daß die McCluskey-Tabelle (Primterm-Minterm-Tabelle) bei großer Argumentenzahl sehr umfangreich wird.

Neuere Methoden vermeiden z.T. diese Einschränkung.

Inhalt

Vorheriges Kapitel

Nächstes Kapitel