| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |
Wie gezeigt wurde, kann eine beliebige
Boolesche Funktion durch einstufige Verknüpfungen von Mintermen
bzw. Maxtermen dargestellt werden.
Diese Form der Funktionsbeschreibung
führt unmittelbar zur Definition sogenannter Normalformen.
Definition:
Hinweis:
Der Begriff "kanonisch"
deutet an, daß die BFkt hier in ihrer einfachsten (und aufwendigsten)
Form beschrieben wird. Häufig sind bei der Funktionsbeschreibung
allerdings Vereinfachungen (s.u.) möglich, so daß die
beschreibenden Terme nicht mehr unbedingt Volldisjunktionen bzw.
Vollkonjunktionen sein werden.
Sowohl eine kDNF als auch eine kKNF werden als zweistufige Schaltungen realisiert. Werden in der Eingangsstufe infolge von Vereinfachungen nicht alle Variablen verknüpft, so wird eine derartige Lösung nicht mehr als "kanonisch" bezeichnet.
Die entsprechenden Normalformen werden dann definiert als:
In verkürzter Form werden beide
auch als disjunktive bzw. konjunktive Form bezeichnet.
Im Englischen haben sich die Begriffe
durchgesetzt.
Hinweis zum Umgang mit Maxtermen:
Der Umgang mit der kanonischen konjunktiven
Normalform (kKNF) fällt erfahrungsgemäß schwer.
Das Grundsätzliche soll deshalb an einem Beispiel noch einmal
dargestellt werden:
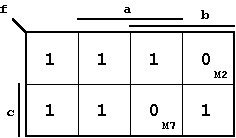
KV-Diagramm einer vorgegebenen Beispiel-BFkt:
| Abb. 2.18: Beispielfunktion. |  |
Die Boolesche Funktion wird also durch sechs 1-Felder und zwei 0-Felder beschrieben.
Da ein Maxterm aber über ein
einzelnes 0-Feld definiert wurde und somit als Volldisjunktion
(Mengenvereinigung) in diesem Falle von sieben 1-Feldern beschrieben
wird, müssen zur Beschreibung obiger Funktion zwei Maxterme
herangezogen werden:
Diese beiden Maxterme sind die folgenden Terme M2 und M7:
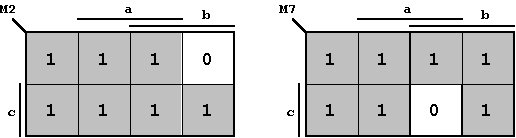
Abb. 2.19: Maxterme zur Beschreibung der Funktion in Abb. 2.18.
Die Überlagerung dieser beiden Maxterme ergibt anschaulich die gesuchte BFkt. Offensichtlich müssen Maxterme konjunktiv verknüpft werden, d.h. es muß die Durchschnittsmenge gebildet werden.
Unter Anwendung der oben eingeführten
Definitionen können die kDNF und kKNF unmittelbar über
eine Wahrheitstafel (Wertetabelle) ermittelt werden.
Funktionsbeispiel:
Die Boolesche Funktion f(a,b,c) sei durch folgende Wertetabelle gegeben:
|
| 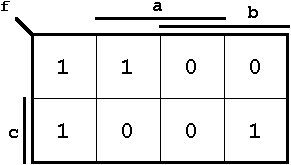 |
a) Bildung der kanonischen disjunktiven Normalform (kDNF):
In der kanonischen disjunktiven Normalform fD
werden alle Vollkonjunktionen (UND-Verknüpfungen) der Eingangsvariablen
a,b,c, die den Funktionswert fD = 1
ergeben, disjunktiv (mit ODER) verknüpft;
hier also:
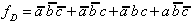 | . (2.1) |
Offenbar wurden nur diejenigen Zeilen
berücksichtigt, für die die Ausgangsvariable den Wert 1 annimmt.
In Minterm-Schreibweise lautet Gl. 2.1 damit:
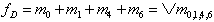 | . (2.2) |
b) Bildung der kanonischen konjunktiven
Normalform (kKNF):
In der kanonischen konjunktiven Normalform
fK
werden alle Volldisjunktionen (ODER-Verknüpfungen) der Eingangsvariablen
a,b,c, die den Funktionswert fK = 0
ergeben, konjunktiv (mit UND) verknüpft;
hier also:
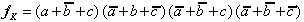 | . (2.3) |
In diesem Fall wurden nur diejenigen
Zeilen berücksichtigt, für die die Ausgangsvariable den Wert 0 annimmt.
In Maxterm-Schreibweise lautet Gl. 2.3 also:
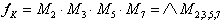 | . (2.4) |
Zusammenfassung:
Eine beliebige Boolesche Funktion f(x1,...,xn) kann immer beschrieben werden als
kDNF (kanonische disjunktive Normalform):
 | (2.5) |
oder als
kKNF (kanonische konjunktive Normalform):
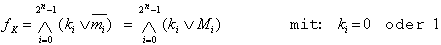 | , (2.6) |
wobei gilt:
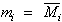
|
| mit: mi = Minterm (Vollkonjunktion),
Mi = Maxterm (Volldisjunktion). |
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |