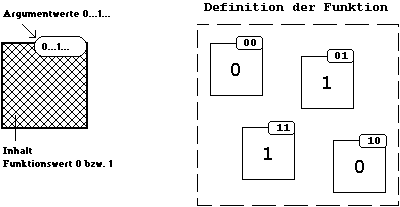
Abb. 2.3: Entwicklung einer grafischen Funktionsbeschreibung.
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |
Als einfachste Form, eine Boolesche
Funktion darzustellen, wurde die Definition durch eine Wertetabelle
(auch Wahrheitstafel genannt) eingeführt.
Eine gegebenen BFkt kann also z.B. wie folgt dargestellt werden:
| | |||||||
Neben den hier aufgeführten Funktionswerten '0' und '1' können auch zwei Sonderfälle
auftreten:
In der Wertetabelle sehen diese beiden Fälle wie folgt aus:
| => beliebig '0' bzw. '1' | |||||||
| => irrelevant |
Diese beiden Sonderfälle haben
besondere Bedeutung bei der Optimierung von Verknüpfungsnetzwerken
(VN's).
Das hier eingeführte tabellarische
Verfahren zur Darstellung Boolescher Funktionen ist genau und
eignet sich besonders gut für eine maschinelle Bearbeitung.
Es besteht aber der Nachteil einer recht unübersichtlichen
formalen Darstellung, in der insbesondere die charakteristischen
Eigenschaften einer BFkt nur schwer zu erkennen sind.
Um die Interpretierbarkeit einer
Funktion zu vereinfachen, wurde von M. Karnaugh und E.W. Veitch
eine grafische Darstellungsform vorgeschlagen, die es erlaubt,
mit Hilfe von Anordnungsmustern und Strukturen unmittelbare Rückschlüsse
auf die BFkt zu ziehen.
Die von Karnaugh und Veitch vorgeschlagene
Darstellung wird heute als Karnaugh-Veitch-Diagramm (kurz KV-Diagramm)
bezeichnet.
Aufbau und Bedeutung dieses Diagramms
werden verständlich, wenn man direkt von der Grunddefinition
einer Booleschen Funktion und deren Mengendarstellung ausgeht.
Für jede BFkt gilt offenbar:
Eine Boolesche Funktion f(a,b,...,x) wird also vollständig beschrieben durch
Damit ist eine grafische Darstellung der BFkt unmittelbar möglich:

Abb. 2.3: Entwicklung einer grafischen Funktionsbeschreibung.
In dieser Grafik definieren die Argumentwerte
die Nummer eines vorgegebenen Rahmens, während der Rahmeninhalt
den zugehörenden Funktionswert wiedergibt.
Zur vollständigen Funktionsdefinition
werden dann alle möglichen Rahmen (Kästchen) angegeben
und zu einer Darstellung zusammengefaßt.
In die oben noch willkürlich
vorgenommene Rahmendarstellung kann Ordnung gebracht werden durch
systematische Definition der Argumente (ähnlich der Achsendefinition
in einem Koordinatensystem). Außerdem werden die zunächst
isoliert dargestellten Kästchen zu einer uniformen Grafik
zusammengefaßt.
Für eine Funktion zweier Argumente f(a,b) ergibt sich folgende grafische Beschreibung:
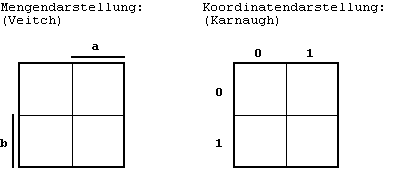
Abb. 2.4: Funktionsgrafik nach Veitch und Karnaugh.
Für die Bezeichnung der Argumente sind hierbei zwei gebräuchliche Methoden aufgezeigt worden:
Beide Darstellungsarten sind natürlich vollkommen gleichberechtigt.
Zur Vervollständigung wird an diesem KV-Diagramm noch die vorgegebene Boolesche Funktion gekennzeichnet.
Beispiel:
| Abb. 2.5: KV-Diagramm (nach Veitch) der bereits bekannten UND-Funktion. | 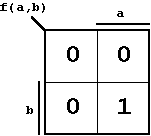
|
Kennzeichnend für das KV-Diagramm ist also:
Diese Eigenschaft wird, ganz anschaulich, als "Nachbarschaftsbeziehung" bezeichnet.
Eine Erweiterung des KV-Diagrammes
über zwei Argumente hinaus ist jetzt möglich, indem
in einfachster Form bereits definierte Karnaugh-Diagramme zu größeren
Feldern zusammengefügt werden. Wichtig ist, daß auch
hierbei die eben definierte Nachbarschaftsregel erhalten bleibt.
Beispiel:
Erzeugung des Karnaugh-Diagrammes
der Funktion f(a,b,c) durch Hinzufügen einer Variablen und
Aneinanderlegen der KV-Teildiagramme:
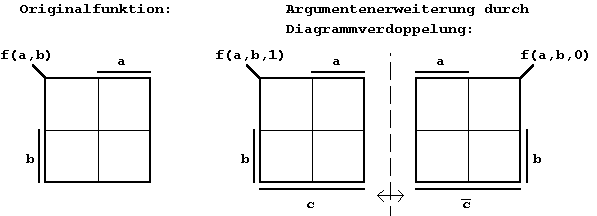
Abb. 2.6: Erweiterung des KV-Diagramms.
Hinweis:
Konstruktionsprinzip größerer KV-Diagramme:
Jede Hinzunahme einer weiteren Variablen hat eine Verdoppelung der Funktionsfelderzahl zur Folge. Beim Zusammenfügen ist die Nachbarschaftsbedingung stets zu beachten: benachbarte Felder unterscheiden sich in nur einem Argumentenwert.
Diese Nachbarschaftsbedingung gilt auch an den Rändern des KV-Diagrammes. Das bedeutet, daß das KV-Diagramm räumlich gesehen einen Zylinder bildet (Abb. 2.8)
.
Für ein KV-Diagramm mit vier Argumenten ergibt sich nachfolgend gezeigte Einteilung.
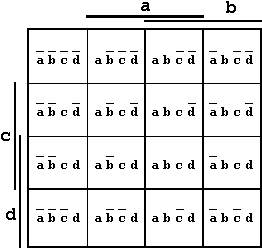
Abb. 2.7: KV-Diagramm mit vier Argumenten.
Die Feldeinträge geben die log. Wertigkeiten der Argumente an den entsprechenden Positionen wieder.
| Abb. 2.8: Räumliche Anordnung eines KV-Diagrammes für drei Argumente a,b,c. | 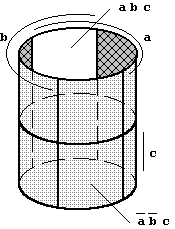
|
Größere KV-Diagramme können in gleicher Form nach dem in Abb. 2.6 gezeigten Schema gebildet werden, wobei entweder sämtliche Argumente in einer Ebene angeordnet werden können (Abb. 2.9) oder aber im Sinne einer verbesserten Übersichtlichkeit in mehreren Ebenen, wodurch sich eine dreidimensionale Struktur ergibt (Abb. 2.10).
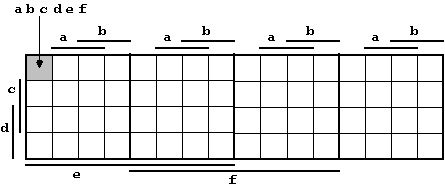
Abb. 2.9: Zweidimensionales KV-Diagramm für sechs Variablen.
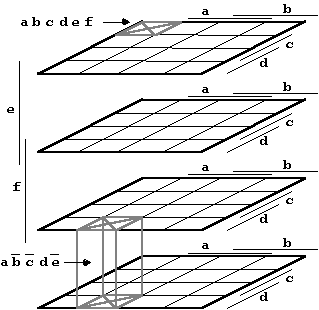
Abb. 2.10: KV-Diagramm für sechs Variablen (in dreidimensionaler Anordnung).
Auf Grund der ansteigenden Komplexität sind KV-Diagramme für die Darstellung von Funktionen mit mehr als sechs Variablen ungeeignet. In diesen Fällen sollten andere Methoden eingesetzt werden (s.u.).
Beispiel:
Die Boolesche Funktion
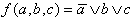
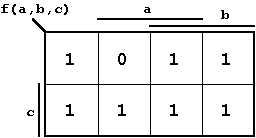
| Abb. 2.11: Boolesche Funktion | 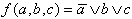 | . |
Die Mengenbetrachtung des KV-Diagrammes
und die damit in Zusammenhang stehenden Bearbeitungsprinzipien
sollen an einem detaillierten Beispiel näher diskutiert werden.
Insbesondere die am KV-Diagramm möglichen Manipulationen
(Vereinfachungen) machen diese Methode zu einem wichtigen Entwurfsinstrument.
Die Übertragung einer BFkt auf ein Karnaugh-Diagramm und die anschließende Bearbeitung
sollen folgende Regeln beachten:
Auf die erzeugten Mengen können dann die bereits bekannten Verknüpfungen Disjunktion,
Konjunktion und Komplementation angewendet werden.
Diese Betrachtungen sollen für die folgende Boolesche Funktion f(a,b,c) durchgeführt werden:
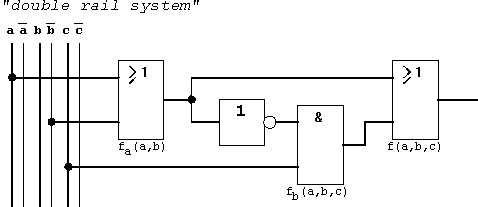
Abb. 2.12: Beispielfunktion im "double rail system".
Hinweis:
In diesem Beispiel liegen die Eingangsvariablen
a, b und c in einem sogenannten "double rail system"
vor. Dies bedeutet, daß sowohl eine vorgegebene Variable
als auch ihre invertierte Form "abgreifbar" zur Verfügung
stehen. Außerdem wird ein ideales Zeitverhalten vorausgesetzt,
d.h. es treten zwischen den Signalen (einschließlich den
invertierten) keine Zeitverzögerungen (s.u.) auf.
Das KV-Diagramm der vorgegebenen BFkt kann jetzt schrittweise aufgebaut werden:
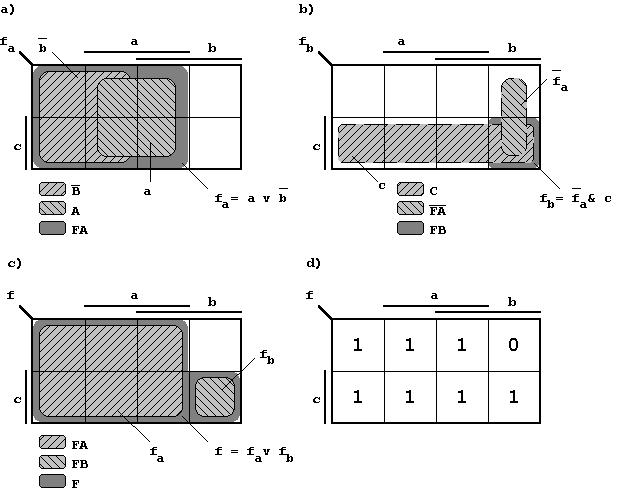
Abb. 2.13: KV-Diagramme zur Bfkt. in Abb. 2.12.
Die KV-Diagramme a) - c) zeigen schrittweise die Ermittlung der Booleschen Funktion f(a,b,c):
Diagramm a:
In diesem Diagramm wird die Menge FA aus Feldern gebildet, für die fa(a,b)=1
ist. Diese Menge ist symmetrisch zur Grenze des Arguments c, d.h.
sie ist unabhängig von c! Dies entspricht der algebraischen
Formulierung der BFkt
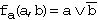 | . |
Diagramm b:
Dieses Diagramm zeigt die Durchschnittsmenge
(Konjunktion) des Komplements von FA und der Menge C (Variable
c='1'). Es entsteht die Menge FB.
Diagramm c:
Im Diagramm c) werden der abschließenden
ODER-Funktion entsprechend die beiden Mengen FA und FB vereinigt
(Disjunktion). Es entsteht die Ergebnismenge F.
Diagramm d:
Dieses Diagramm reformuliert das Ergebnis c) in der gewohnten Darstellung des KV-Diagramms.
Das Ergebnis der Analyse dieses 4-stufigen Verknüpfungsnetzes ergibt eine Boolesche Funktion, die nur für den Fall a = c = 0 und b = 1 eine '0' erzeugt, für alle anderen Fälle aber eine '1' generiert (siehe Diagramm d). Diese Eigenschaft entspricht der bereits bekannten ODER-Funktion (Disjunktion).
Es zeigt sich also, daß die
vorgegebene Originalfunktion durch ein einziges ODER-Gatter ersetzt
werden kann, ohne daß das logische Verhalten sich ändert.
Das Verknüpfungsnetz wird dabei außerdem auf eine Stufe
reduziert (1-stufig), die Signallaufzeit reduziert sich dementsprechend
(auf eine Gatterlaufzeit, s.u.).
Ergebnisschaltung:
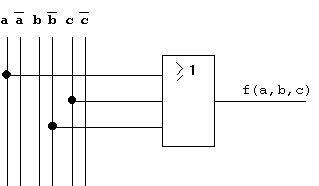
Abb. 2.14: Reduzierte Form der Schaltung in Abb. 2.12.
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |