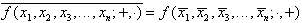 |
(1.31), |
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |
1.7 Dualitätsprinzip und Boolesche Verbände
Aus den in Kapitel 1.6 eingeführten
Booleschen Postulaten und Theoremen lassen sich wichtige Verallgemeinerungen
ableiten, die für die Digitaltechnik von fundamentaler Bedeutung
sind.
Aus den in Form von Postulaten aufgestellten Grundforderungen an eine Boolesche Algebra kann das Prinzip der
Dualität hergeleitet werden.
Dualitätsprinzip:
Zu jeder Aussage, die auf die Booleschen Postulate zurückgeführt werden kann, existiert eine duale Aussage, die durch gleichzeitiges Vertauschen der Operationen "+" und "·" sowie der Einzelelemente "0" und "1" entsteht.
Dieses Prinzip folgt natürlich unmittelbar aus dem symmetrischen Aufbau der Postulate bezüglich
der entsprechenden Operationen und Elemente.
Insbesondere ist das De Morgansche Theorem eine Dualitätsaussage. Unter Benutzung der drei Funktionen
"+", "·" und "Negation" kann dieses Theorem verallgemeinert werden:
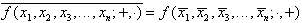 |
(1.31), |
wobei f eine Boolesche Funktion darstellt und xi Boolesche Variablen sind.
In modifizierter Form kann mit Hilfe obiger Beziehung der Begriff der "dualen Operationen"
(dualen Funktionen) eingeführt werden:
Definition: dual
Zwei Operationen f1 und f2 sind dual zueinander, wenn gilt:
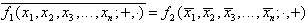 |
(1.32). |
Zwei Funktionen sind also dual zueinander, wenn sie durch Vertauschen der 0- und 1-Elemente ineinander übergehen:
Beispiel:
Es soll die duale Funktion der UND-Funktion durch Invertierung der Einzelelemente gebildet werden.
Dies kann z.B. durch Benutzung von Wahrheitstafeln (Funktionstabellen) in sehr einfacher Weise durchgeführt
werden:
Die linke Funktionstabelle gibt die UND-Funktion wieder. Die rechte Tabelle zeigt die gleiche Funktion
nach der Umwandlung. Die zweite Tabelle entspricht offenbar genau der bereits bekannten ODER-Funktion:
Ergebnis:
Die Konjunktion (UND) und die Disjunktion (ODER) sind dual zueinander.
Die Gesamtheit der oben eingeführten
hat in der Mathematik eine besondere Bedeutung. Sie wird als Boolescher Verband bezeichnet. Die Wichtigkeit dieser drei Verknüpfungen liegt darin, daß allein mit ihnen jedes Problem der Aussagenlogik gelöst werden kann. Das aus "UND", "ODER" und "NOT" gebildete System wird deshalb auch als "vollständiges Logik-System" bezeichnet.
Diese Aussage entspricht natürlich unmittelbar der Tatsache, daß zur Beschreibung der Booleschen
Algebra lediglich diese Funktionen bzw. die zugehörigen Operatoren (,,¯) notwendig sind.
Für die Praxis ist diese Beschränkung auf nur drei Grundfunktionen von außerordentlicher Konsequenz, zeigt sie doch, daß zur Realisierung jeder beliebigen Schaltung nur eben diese Funktionen benötigt werden. Das wiederum heißt, daß man sich beim Entwurf von Schaltungen auf einige wenige Bauteile beschränken kann.
Letztendlich führt diese Tatsache zur Einführung sogenannter "universeller Logik-Blöcke",
die wiederum die Grundlage für die "Programmierbare Logik" bilden (s.u.).
Die Definition eines vollständigen Systems ist allerdings nicht auf diese drei Grundfunktionen beschränkt.
Ein solches Systems kann sogar durch eine einzige Funktion voll bestimmt werden. Funktionen, die diese Eigenshaft besitzen sind
die negierten Formen der Funktionen "UND" bzw. "ODER",
die als "NAND" (Not-AND) bzw. "NOR" (Not-OR) bezeichnet werden.
Auf Grund ihrer besonderen Wichtigkeit hat man ihnen ihren "Entdeckern" zu Ehren besondere
Namen verliehen:
| NAND | = | Sheffer-Funktion |
| NOR | = | Peirce-Funktion |
Jede dieser beiden Funktionen alleine bildet also ein vollständiges System. Da die gesamte Schaltalgebra
durch die Operationen "UND", "ODER" und "NOT"
definiert ist, reicht es zum Beweis, zu zeigen, daß eben diese Funktionen mit Hilfe der Sheffer- bzw. der Peirce-Funktionen
aufgebaut werden können.
Beweis für Aufbau mit der Sheffer-Funktion
(NAND):
| Negation: | 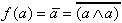 |
| UND: | 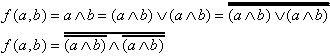 |
| ODER: | 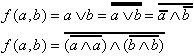 |
Bei Benutzung von NAND-Gattern ergeben sich dafür die folgenden Realisierungen:
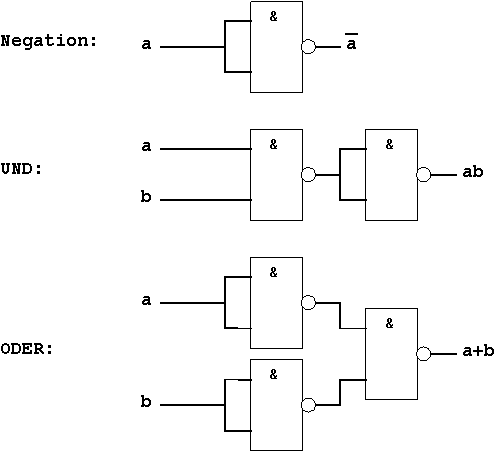
Abb. 1.34: NAND-Darstellung von Negation, UND, ODER.
Darüberhinaus können auch die notwendigen Konstanten "0" und "1" mit
Hilfe der Sheffer- oder Peirce-Funktion realisiert werden:
Beweis für Realisierung mit der Sheffer-Funktion (NAND):
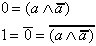
Auf Grund der Tatsache, daß dieses System auch die beiden Konstanten erzeugt, wird es als
"stark vollständiges System" bezeichnet.
Es wurde damit also gezeigt, daß sich sämtliche logischen Schaltungen aus einem einzigen Baustein (z.B. einem NAND) aufbauen lassen.
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |