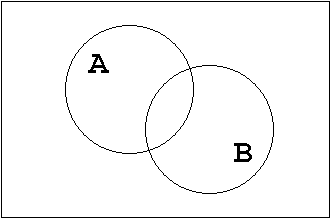
Abb. 1.19: Kommutativgesetz.
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |
Die Booleschen Funktionen sollen
jetzt einer genaueren Behandlung unterzogen werden, insbesondere
soll die zweielementige Boolesche Algebra präziser definiert
werden.
Zur Definition einer Booleschen Algebra
können prinzipiell zwei unterschiedliche Wege beschritten
werden. Es kann entweder von der Verbandstheorie oder von einem
Axiomensystem ausgegangen werden.
Hier soll der axiomatische Weg verfolgt werden, wobei ein System benutzt wird, das von dem amerikanischen
Mathematiker Huntington 1904 entwickelt wurde.
Bei der Behandlung des Axiomensystems kann kann eine Unterteilung in die
1.6.1 Die Booleschen Postulate
Die Booleschen Postulate stellen formal die Forderungen zusammen, die eine Boolesche Algebra erfüllen
muß.
Definition:
Die Boolesche Algebra ist die Menge A mit den Elementen 0 und 1, in der die zweielementigen Operationen
"+" und "·" (bzw. "" und "")
definiert sind, so daß gilt:
Unter Heranziehung der Booleschen Postulate können jetzt die Booleschen Theoreme (Lehrsätze)
aufgestellt werden. Die Richtigkeit dieser Lehrsätze kann
jederzeit mit Hilfe der Postulate überprüft werden (z.B
unter Verwendung von Wahrheitstafeln).
Ein Theorem in der Booleschen Algebra
ist eine Regel, die eine fundamentale Beziehung zwischen den Booleschen
Variablen zum Ausdruck bringt. Anwendung der Theoreme wird es dann erlauben, logische Schaltungen
in vielfältiger Form zu manipulieren bzw. zu vereinfachen.
Zur Definition und Diskussion der einzelnen Theoreme soll jeweils von drei Aspekten ausgegangen werden:
T1: Kommutativgesetz (Vertauschungsgesetz)
T1.1
| a) | a + b = b + a | |
| b) | a · b = b · a |
T1.2 Mengendarstellung:

Abb. 1.19: Kommutativgesetz.
Plausibilitätsbetrachtung:
Es ist offenbar gleich, in welcher Reihenfolge die Mengen A und B disjunktiv ("+") bzw.
konjunktiv ("·") verknüpft werden.
T1.3 Gatter-Implementierung:
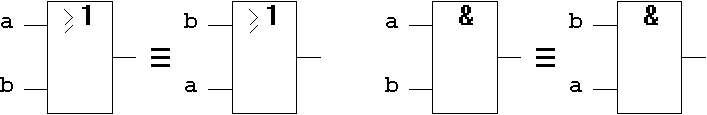
Abb. 1.20: Kommutativgesetz auf Gatterebene.
Plausibilitätsbetrachtung:
Es ist offenbar gleich, in welcher Reihenfolge die Eingangsvariablen an die Eingänge der ODER-
bzw. UND-Gatter gelegt werden.
T2: Assoziativgesetz
T2.1
| a) | (a + b) + c = a + (b + c) | |
| b) | (a · b) · c = a · (b · c) |
T2.2 Mengendarstellung:
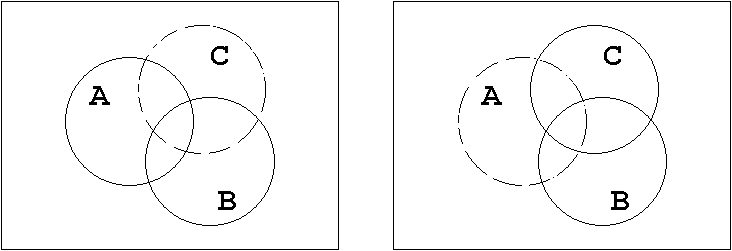
Abb. 1.21: Assoziativgesetz.
Plausibilitätsbetrachtung:
Es ist offenbar gleich, in welcher Reihenfolge die Mengen A, B und C disjunktiv ("+") bzw.
konjunktiv ("·") verknüpft werden.
T2.3 Gatter-Implementierung:
Jeder Klammerung, die in der algebraischen Form auftritt, entspricht bei der Gatterimplementierung eine Gatterebene (der entsprechende algebraische Ausdruck wird als "gatterisomorph" bezeichnet).
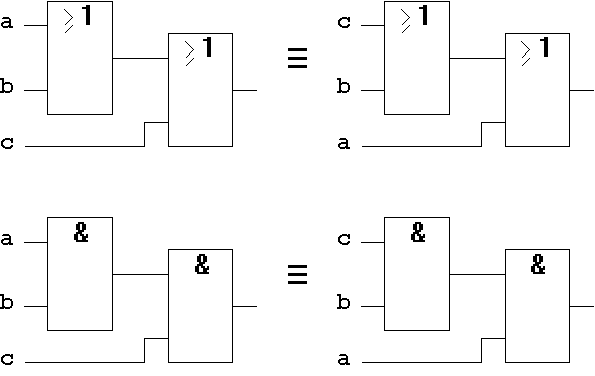
Abb. 1.22: Assoziativgesetz auf Gatterebene.
T3: Distributivgesetz (Verteilungsgesetz)
Die Funktionen "Disjunktion" und "Konjunktion" sind distributiv (verteilend), d.h.
"ODER" verteilt sich über "UND, "UND"
verteilt sich über "ODER".
T3.1
| a) | a + (b · c) = (a + b) · (a + c) | |
| b) | a · (b + c) = (a · b) + (a · c) = a · b + a · c |
Aussagenlogisch bedeutet dies im Falle von Form a):
Der Ausdruck "a + (b ·
c)" ist genau dann wahr, wenn "a" wahr ist oder
wenn "b" und "c" beide wahr sind.
"(a + b) · (a + c)"
ist genau dann wahr, wenn jeder der beiden Klammerausdrücke
wahr ist. Diese Ausdrücke sind wiederum wahr, wenn "a"
wahr ist. Ist "a" nicht wahr, so müssen "b"
und "c" beide wahr sein.
Entsprechend kann algebraische Form b) interpretiert werden.
T3.2 Mengendarstellung:
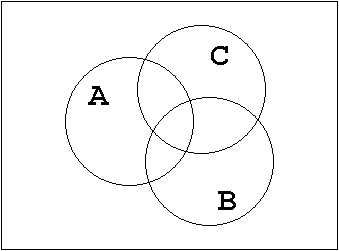
Abb. 1.23: Distributivgesetz.
Plausibilitätsbetrachtung:
Durch schrittweises Vorgehen kann die Richtigkeit des Distributivgesetzes an Hand des Mengendiagrammes
veranschaulicht werden.
T3.3 Gatter-Implementierung:
Durch Anwendung dieses Theorems T3 kann die Anzahl der Gattereingänge (engl. pin count)
einer Schaltung reduziert werden.
Form a):
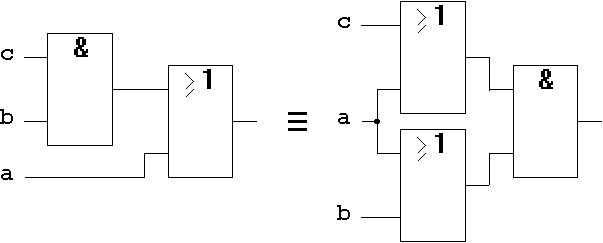
Abb. 1.24: Distributivgesetz auf Gatterebene.
Für Form b) kann die Gatterimplementierung in ähnlicher Weise vorgenommen werden.
T4: Idempotenzgesetz (Identitätsgesetz)
T4.1
| a) | a + a = a | |
| b) | a · a = a |
T4.2 Mengendarstellung:
Die Menge bleibt bei disjunktiver bzw. konjunktiver Verknüpfung mit sich selbst unverändert.
T4.3 Gatter-Implementierung:

Abb. 1.25: Idempotenzgesetz auf Gatterebene.
Die Gatterschaltung ist logisch redundant.
Sie verzögert allerdings das Signal "a" und hat damit technische Bedeutung.
T5: Absorptionsgesetz (Verschmelzungsgesetz, Redundanzgesetz)
T5.1
| a) | a + (a · b) = a | |
| b) | a · (a + b) = a |
Aussagenlogisch bedeutet dies
für den Ausdruck "a + (a · b)":
Ist "a" wahr, dann ist
der Wert von "b" irrelevant. Ist jedoch "a"
falsch, kann (a · b) nicht mehr wahr werden. Der Ausdruck
ist also vollständig durch "a" bestimmt, "b"
wird "absorbiert".
für den Ausdruck "a · (a + b)":
Ist "a" wahr, dann ist
auch "(a + b)" wahr, d.h. der gesamte Asudruck ist wahr.
Ist "a" falsch, so ist der gesamte Ausdruck falsch.
Der Ausdruck ist also wiederum vollständig durch "a"
bestimmt, "b" wird "absorbiert".
Dieses Gesetz folgt unmittelbar aus dem Distribtivgesetz unter Einbeziehung des Idempotenzgesetzes (T3 und T4).
T5.2 Mengendarstellung:
Auch am Venn-Diagramm kann die logische
Redundanz der Schaltung überprüft werden.
T5.3 Gatter-Implementierung:
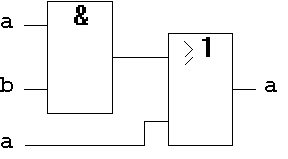
Abb. 1.26: Absorptionsgesetz auf Gatterebene.
Die Gatterschaltung ist wiederum logisch redundant. Wie später gezeigt wird, verzögert
sie aber das Signal "a" um zwei Gatterlaufzeiten und hat damit eine technisch relevante Funktion.
T6: Null- und Eins-Gesetz
T6.1
| a) | 0 + a = a 1 + a = 1 | |
| b) | 0 · a = 0 1 · a = a |
T6.2 Mengendarstellung:
Die Verifikation dieses Theorems durch Venn-Diagramme ist natürlich trivial.
T6.3 Gatter-Implementierung:
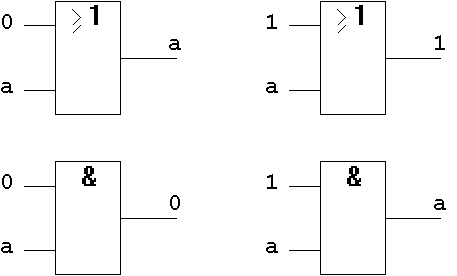
Abb. 1.27: Null- und Eins-Gesetz auf Gatterebene.
T7: Komplement-Gesetz
Zu jedem Element "a" existiert ein komplementäres Element "\a".
"\a" wird Komplement von "a" genannt.
T7.1
| a) | a + \a = 1 | |
| b) | a · \a = 0 |
T7.2 Mengendarstellung:
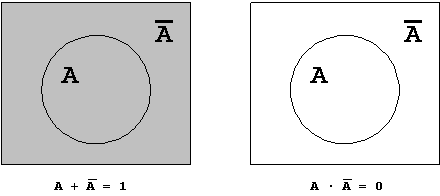
Abb. 1.28: Komplement-Gesetz.
T7.3 Gatter-Implementierung:
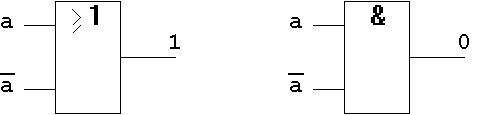
Abb. 1.29: Null- und Eins-Gesetz auf Gatterebene.
T8: De Morgansches Theorem
T8.1
| a) | 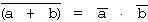 |
|
| b) | 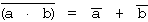 |
Das De Morgansche Theorem hat sehr große Bedeutung für die Schaltungstechnik. Insbesondere bei der Transformation von Schaltungen kommt die in diesem Gesetz ausgedrückte Möglichkeit der Umwandlung zwischen unterschiedlichen, sogenannten dualen Booleschen Funktionen zur Anwendung:
Wie die oben wiedergegebenen algebraischen Formen verdeutlichen, ist die Umwandlung von NOR- zu UND-Schaltungen
bzw. von NAND- zu ODER-Schaltungen unmittelbar möglich:
NOR UND
NAND ODER .
Dieser Sachverhalt wird besonders deutlich an der Gatterimplementierung:
T8.3 Gatter-Implementierung:
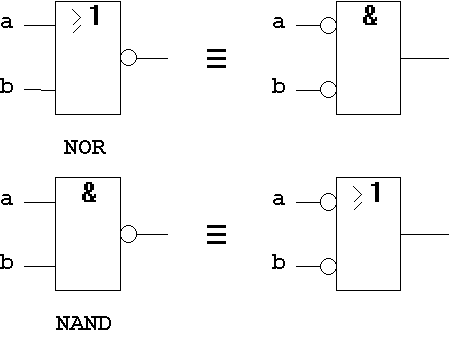
Abb. 1.30: De Morgansches Theorem auf Gatterebene.
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |