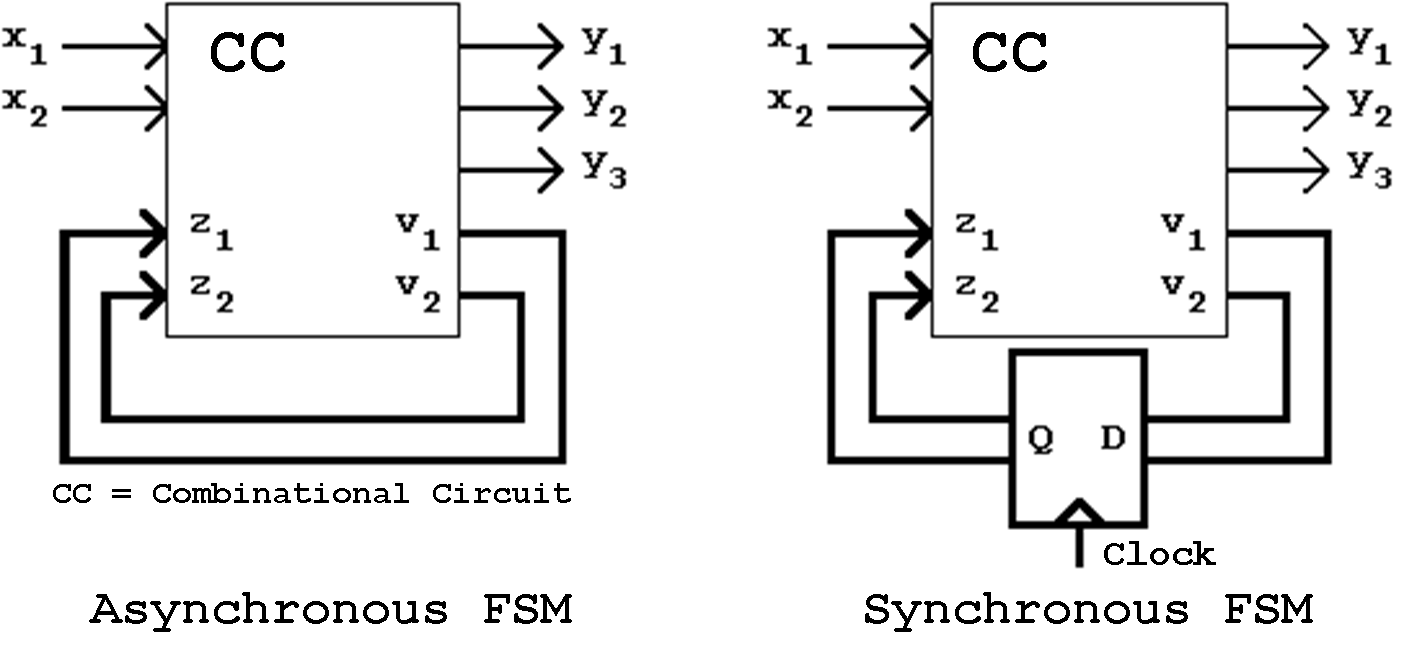
Figure 6.1: Asynchronous and Synchronous Finite State Machine
| Contents | Previous Chapter | Next Chapter |
In connection with the treatment of Flip-Flops it has been shown that sequential logic circuit are built from combinational circuits adding storage capabilities. The logic of the sequential circuit is implemented with the combinational circuits, the storage effect represents the switching history (the past behaviour).
For a sequential system the amount of information that can be stored is “finite” and the “total number of different possible states” this information can be in is also finite. Because of this a sequential circuit is also known as a Finite State Machine (FSM). The behaviour of this circuit can be described using an FSM model. A Finite State Machine is an abstract model consisting of a finite set of states, the transitions between those states, and the actions to be performed while in those states
or during transitions between states.
A typical example of a sequential circuit is the modulo-4 counter (see above), in which a new counter value is determined knowing the old one. The input signals (pulses) are just triggering the event
To realize the storage capability in an FSM two possibilities exist:

Figure 6.1: Asynchronous and Synchronous Finite State Machine
Finite State Machines with direct feedback (without explicit storage elements) are called asynchronous FSMs, Finite State Machines with explicit flip-flops or registers in the feedback path are called (clock) synchronous FSMs.
To describe the sequences in a finite state machine and thus the distinct behaviour of the two basic FSM types the term state gets a central meaning. The state describes the current behaviour of the finite state machine. This present state is the logical consequence of all the previous states of the FSM and the current external data inputs. For the subsequent state it again represents the complete previous history of the FSM.
The states of an FSM can be of different duration, therefore it is possible to distinguish:
During the operation of asynchronous FSMs an important basic rule covering the application of combinational circuits is abolished:
At the feedback inputs the signal values can already change while the signal waves within the combinational circuit are still active and consequently the circuit activities did not assume stable values yet.
Finite State Machine (FSM) Terminology:
| Contents | Previous Chapter | Next Chapter |