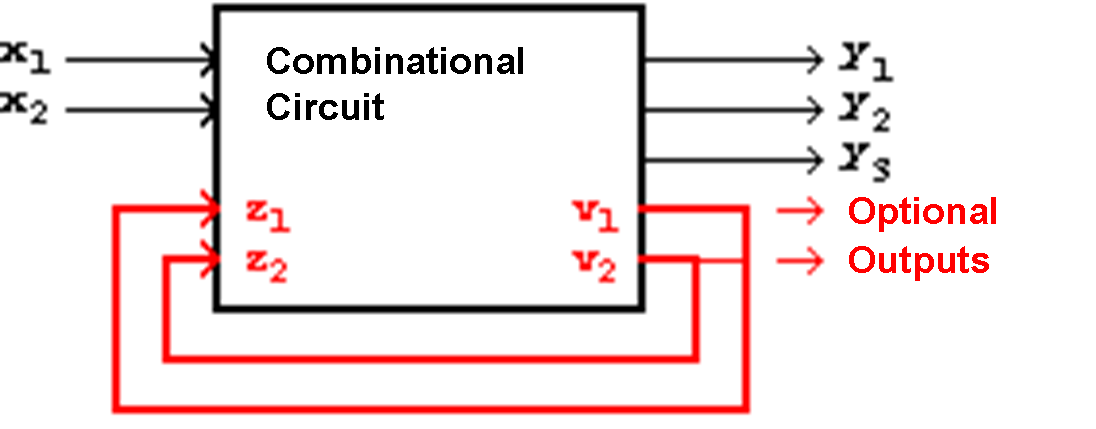
Figure 4.1: Switching Circuit with Feedback.
| Contents | Previous Chapter | Next Chapter |
The combinational circuits treated so far can be completely characterized by the actual values on their input parameters. This information alone is sufficient to determine all output parameter values. Circuits of this type do not contain any internal storage elements.
For such combinational circuits the following limitations are (implicitly) valid:
In order to abolish these limitations feedbacks will now be introduced, so that circuits of the following type will be possible:

Figure 4.1: Switching Circuit with Feedback.
Circuits of this kind can be described in the known way, e.g. using truth tables, but the internal states vi and zi must now be taken into consideration. These internal states affect the outputs yi. Therefore another differentiation has to be done in stable and unstable states:
feedback | ||||||||
Thus circuit inputs as well as circuit outputs form two classes, respectively:
The distinctive feature are the feedback signals that trigger the following sequence of events in the circuit:
In the stable state of the system a change of an input signal may occur. When this causes a change of the feedback output
vi, then the circuit input zi will also change.
For the subsequent process two cases can be distinguished:
It has to be observed at this point that the signal changes can occur at the feedback inputs at a time when not all internal signal changes have reached the circuit outputs.
Thus the second limitation defined above has been removed, too. Also those signals have now to be considered that change at the circuit inputs at different times. Thus very complicated processes can occur in the switching circuits that are determined by the gate propagation delay times.
The circuits with feedback shown here are called sequential logical circuit (in contrast to the simple combinational circuits).The signals can cycle through those sequential logical circuits several times until finally a stable state is reached.
The term "state" plays a central role at this point. It is used in its colloquial form, describing the current state of the sequential circuit. It is the logical consequence of all the previous states and the current external inputs of the sequential circuit. Consequently it represents for the subsequent state the entire previous status (history) of the circuit .
| Contents | Previous Chapter | Next Chapter |