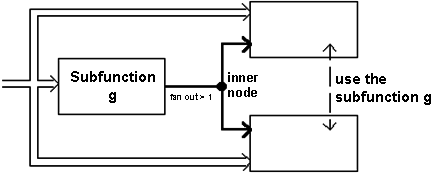
Figure 2.33: Definition and application of subfunctions.
| Contents | Previous Chapter | Next Chapter |
So far only the possibility for the realization of single functions has been investigated.
Not least because of the complexity of digital devices it may sometimes be advisable to realize several Boolean Functions jointly in one device network. A relation between these Boolean Functions should e.g. exist through arguments that these functions have in common. Then it is possible during the circuit realization to look for further similarities that can be used to reduce the circuit complexity.
Definition:
We call a Boolean lattice (a combinational network) a Function Bundle when it realizes several Boolean functions. In this case the circuit has more than only one output.
A reduction of complexity can then be achieved by identifying subfunctions that can be used simultaneously by several functions. Prerequisite for this type of signal distribution is the existence of several internal nodes. But these nodes can lead to two disadvantages:

Figure 2.33: Definition and application of subfunctions.
Example:
In the above example function used to introduce the idea of "don't care" cases, besides the Boolean function f(a,b,c,d) a second Boolean function g(a,b,c,d) will be realized:
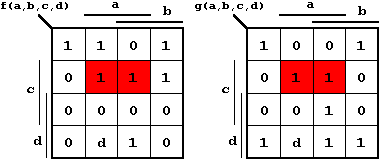
Figure. 2.34: Using shared subfunctions.
As can be easily seen, it is possible to share the group formed out of m5 and m7. Furthermore the "don't care" field can advantageously be defined as:
| f(1,0,0,1) = 1 , | |
| g(1,0,0,1) = 0 . |
| Contents | Previous Chapter | Next Chapter |