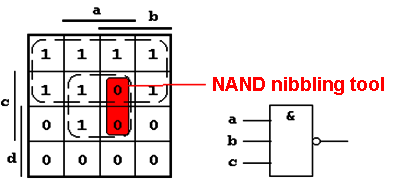
Figure 2.30: Using the NAND "Nibbling Tool".
| Contents | Previous Chapter | Next Chapter |
During the realization and simplification of a Boolean Function the following situation can occur:
Example:

Figure 2.30: Using the NAND "Nibbling Tool".
The groups marked with dashed lines in the M-Map correspond to the following DNF realization:
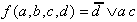 | . | (2.13) |
Obviously this Boolean Function does not correspond to the example function, because in the marked group the two required '0' elements are not produced. This can be corrected using the "nibbling tool" that will cut out the two wrong '1' fields. Obviously a typical application for this kind of tool.
This nibbling tool can easily be implemented using a NAND gate that produces a '0' for a=b=c=1, what means that it will cut out the two unneeded '1' values.
Algebraically seen a conjunctive combination of the oversized '1' field with the NAND nibbling tool is necessary, what results in the final Boolean Function:
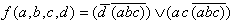 | (2.14) |
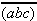 |
represents the "nibbling tool" | (2.14) |
or, using a NAND implementation:
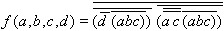 | (2.15) |
It may happen that for certain argument values the Boolean Function does not have a unique solution value. This occurs when on the basis of the given problem certain argument values are not generated. Consequently it is irrelevant for the circuit application whether for the corresponding argument values an output '0' or '1' is produced. This case is called a "don't care".
For the K-Map this "don't care" case means that the corresponding position can arbitrarily be filled with a '0' or a'1' value. For the circuit realization this means an additional degree of freedom, because the value of this field can be optimised depending on the neighbouring fields in such a way, that the formation of as large as possible prime implicants becomes feasible.
Example:
The following function may be given:
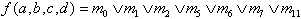 | . | (2.16) |
| Mm9 may be "don't care". |
In this example the function is defined using minterms, based on the following indexation of the K-Map fields:
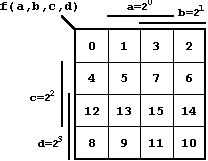
Figure. 2.31: Minterm Indexation for 4 Variables.
With this definition the K-Map of the Boolean Function can be specified:
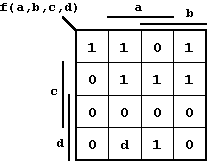
Figure 2.32: K-Map of the Boolean Function specified in Equ. 2.16.
In this case m9 (d = '1') is partner neighbour of m1 and m11, respectively; a core prime implicant (essential) can be formed out of m9 and m11, and a relatively eliminable prime implicant out of m9 and m1. Therefore the solution is (as DNF):
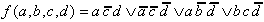 | (2.17) |
In a similar way M9 (d = '0') can be interpreted as partner of M8, M12, and M13, which allows the formation of an additional core prime implicant. In this case the solution is (CNF):
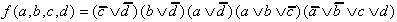 | (2.18) |
This example shows how in a predefined M-Map an existing "don't
care" field can be realized either as a minterm or as a maxterm, to allow the formation of groups as large as possible. Naturally, the
"don't care" field will not be introduced, in order to produce an additional minterm or maxterm in a DNF or CNF.
Looking at these two solutions derived above, it can be shown how another parameter that is important for the circuit implementation can be minimized through the formation of groups: the number of gate inputs c, the so-called pin count.
| cDNF (for comparison) | c = 7·4 + 7 = 35 |
| DNF | c = 4·3 + 4 = 16 |
| CNF | c = 3·2 + 3 + 4 + 5 = 18 |
In the minimized (grouped) solutions (DNF
or CNF) the use of a "double rail" system is assumed.
| Contents | Previous Chapter | Next Chapter |