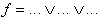2 Combinational Circuit Design

2.6 Summary

Fundamental Description of Boolean Functions

In order to simplify (minimize) a Boolean function using Karnaugh Diagrams (K-Maps), the combination (grouping) of fields (boxes, squares) is necessary. This process can be applied to the 0-fields or the 1-fields. Furthermore, to characterize these fields the arguments or their complements can be used.

As can be seen, a multitude of combinations can be distinguished. These possibilities will be summarized here.

2.6.1 Combination of 1-Fields

Describing a Boolean function using 1-fields:

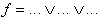		DNF (AND/OR-Form) - SOP
	Transformation using the "de Morgan" Theorem results in:
		(NAND-Form)

Figure 2.25: Description using 1-Fields (SOP - Sum-of-Products Form).

Describing a Boolean function using the complement of 1-fields:

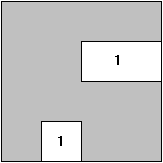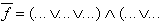		(OR/AND-Form)
	Transformation using the "de Morgan" Theorem results in:
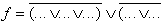		(NOR/OR-Form)

Figure 2.26: Description using Complements of 1-Fields.

2.6.2 Combination of 0-Fields

Describing a Boolean function using 0-fields:

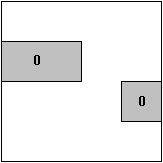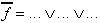		(AND/OR-Form)
	Transformation using the "de Morgan" Theorem results in:
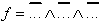		(NAND/AND-Form)

Figure 2.27: Description using 0-Fields

Describing a Boolean function using the complement of 0-fields:

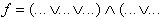		CNF (OR/AND-Form) - POS
	Transformation using the "de Morgan" Theorem results in:
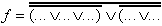		(NOR-Form)

Figure 2.28: Description using Complements of 0-Fields (POS - Product-of-Sums Form).

2.6.3 Transformation of AND/OR Circuits

Considering two-level implementations (of circuits), the AND/OR-Form (DNF) and the OR/AND-Form (KNF) are of special importance, because they represent very straightforward description forms.

Definition:

A multilevel network with an arbitrary number of inputs and outputs is called an AND/OR-network when on any arbitrary signal path between an input and an output AND and OR functions are alternatingly passed.

Example:

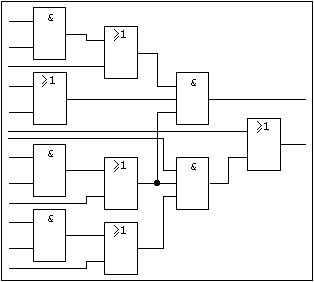
Figure 2.29: Typical AND-OR-Network.

Considering practical applications, circuits implemented with NAND or NOR gates, respectively, are more important than AND/OR networks. The main reason for this is a technological one: basic NAND and NOR gates can be manufactured more easily.

Therefore the transformation from AND/OR/NOT-circuits to NAND/NOR-circuits is of very high importance. This transformation follows again the "DeMorgan" Theorem and can therefore be formulated as a simple three-step process:

AND/OR functions are replaced by NAND or NOR functions, respectively.
Network inputs that belong to OR or AND functions, respectively, are inverted.
Network outputs of AND or OR functions, respectively, are inverted.

Transformation Example (two-level networks):

AND/OR → NAND:

(2.11)

OR/AND → NOR:

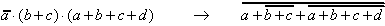(2.12)

Contents

Previous Chapter

Next Chapter