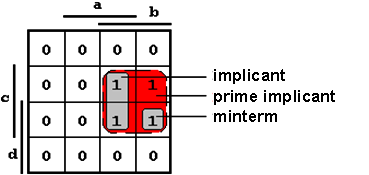
Figure 2.22: Definition of Implicants.
| Contents | Previous Chapter | Next Chapter |
The groupings (combinations) of adjacent fields can indicate important properties of a Boolean function. These properties depend on the size of the group and the relationship between the groups. In order to better understand their characteristics, different forms of groupings can be differentiated. This leads to the following definitions:
Definition: Implicant
An implicant is a grouping of fields (boxes) in the Karnaugh Map or the corresponding algebraic term. The term "Implicant" can be considered synonymous with the terms used to indicate groupings of fields in the K-Map (group, box, etc.).
Definition: Prime Implicant (PI)
The implicant of a Boolean function is called a Prime Implicant when it is not completely contained in another implicant.
Definition: Essential (or Core) Prime Implicant (essential PI)
When a Prime Implicant (PI) contains at least one complete conjunction (a '1' field) which is not part of another PI, then this PI is called an "Essential (or Core) Prime Implicant".

Figure 2.22: Definition of Implicants.
As can be verified with simple examples, it is normally possible to form various implicants, prime implicants, and essential prime implicants. Obviously the question is coming up, which of these implicants definitely have to be considered for a circuit realization.
Rule:
This leads to the definition of two more terms:
Definition: Absolutely Eliminable Prime Implicant
A PI is absolutely eliminable, when for the given Boolean function a disjunction of essential PIs exists, in which it is completely contained.
Definition: Relatively Eliminable Prime Implicant
A PI is relatively eliminable, when it is neither an essential PI nor an absolutely eliminable PI. A part of the relatively eliminable PIs must be considered in the circuit realization (hence the term "relative").
To find the minimal form of a Boolean function (at this point this should be the realization with the smallest number of gate inputs) the following class division or hierarchy can be used, to decide the implicants that have to be considered:
Example: Classification of Implicants:
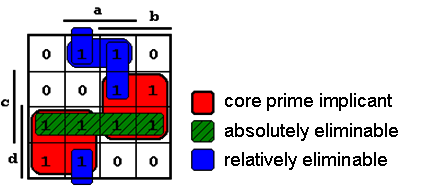
Figure 2.23: K-Map with categorized Implicants.
To describe the Boolean function two minimal forms are possible that differ only in the selection of the relatively eliminative PIs:
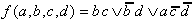 |
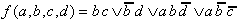 | . |
Note:
All the rules that have been defined for the 1-groups are valid in equivalent form for 0-groups..
2.5.1 Quine-McCluskey Method
Beyond the graphical approach to find the prime implicants some algorithmic methods do exist to find the solution to this problem. The best known method goes back to Quine and McCluskey. The minimization technique named after them can be compared with the K-Map procedure, because both methods go back to the same algorithmic principles..
But the Karnaugh-Veitch method has the disadvantage that because of the graphical method the number of arguments should be limited to a maximum of five to six. Furthermore it is not possible to decide about the absolute minimal (i.e. optimal) realization when several similar minimal forms exist.
The Quine-McCluskey Method proceeds in a very similar form, but applies an exactly definable table-based procedure, to determine the prime implicants of the Boolean function. This first sub-step goes back to Quine. A likewise graphical extension was later introduced by McCluskey, in order to select from these prime implicants those that must be considered for the minimal realization.
2.5.1.1 Quine Method
Like the Karnaugh-Veitch method this procedure is based on the equation
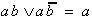 | , | (2.7) |
which lead to the neighbour relation and the resulting simplification possibility in the K-Map.
The Quine method starts with a canonical Normal Form of the Boolean function, e.g. a cDNF. All minterms (elementary conjunctions) of this cDNF are arranged in a table, initially grouping them according to the number of '1' values (i.e. the non-inverted arguments). Within the individual groups the order is arranged according to the weight.
The function shown in the following K-Map will be used to explain in detail this first step.
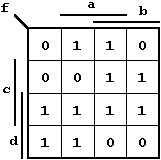
Figure 2.24: Karnaugh Diagram of Example Function.
The minterms, described using the arguments "dcba"
are organized in a table and grouped according to the number of '1' values:
 | |||
 | |||
 | |||
 | |||
 | |||
 | |||
 | |||
 | |||
 | |||
 | |||
Table 2.1: Grouped Minterm Table.
To apply equation (2.7) , pairs of those minterms have to be identified that differ in only one argument. This means that in Table 2.1 only minterms in adjacent groups have to be compared. In those pairs that fulfil this condition the the differing argument can be eliminated.
The elimination of this argument is marked in Table 2.1 (using a tick mark) and carried out in a second table using a dash in place of the eliminated argument.
 | |||
 | |||
 | |||
 | |||
 | |||
 | |||
 | |||
 | |||
 | |||
 |
Table 2.2: Grouping Table after 1st Simplification.
This process will be repeated as long as eliminations are possible. The following table shows this for the example:
Table 2.3: Grouping Table after 2nd Simplification.
As can be seen from Table 2.3 another elimination is not possible in this case. The tabular process introduced by Quine is terminated.
Those terms that where not checked off(tick mark) in the elimination tables are the looked-for prime implicants of the Boolean function.
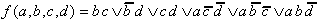 | . |
Obviously these are all the existing prime implicants, also including those that are not necessary for the realization of the function.
At this point the selection process developed by McCluskey comes into action.
2.5.1.2 McCluskey Method (Technique)
Again, this technique is organized in a tabular form. To select the necessary implicants all minterms are presented in a table adjacent to the prime implicants that were found.
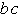 |
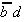 | 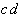 | 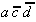 |
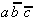 | 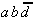 | ||
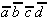 |
|||||||
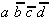 |
|||||||
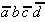 |
|||||||
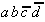 |
|||||||
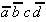 |
|||||||
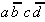 |
|||||||
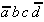 |
|||||||
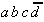 |
|||||||
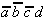 |
|||||||
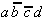 |
|||||||
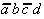 |
|||||||
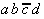 |
|||||||
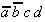 |
|||||||
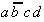 |
|||||||
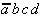 |
|||||||
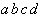 |
|||||||
Table 2.4: Selection Table according to McCluskey
(dark (red) cells mark Core Prime Implicant columns).
To begin with, those minterms can be determined that appear in only one prime implicant. Obviously these selected prime implicants are core (essential) prime implicants, that have to be considered in the circuit design.
For further processing those (considered essential) core prime implicants can be removed from Table 2.4, the corresponding columns and rows with already realized minterms can be eliminated.
The resulting reduced Table 2.5 shows:
The prime implicant 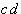 is redundant and therefore absolutely eliminable (all minterms have already been realized).
is redundant and therefore absolutely eliminable (all minterms have already been realized).
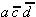 ,
, 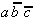 and
and 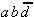 are relatively eliminable, only
are relatively eliminable, only 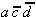 has to be realized or
has to be realized or
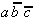 together with
together with 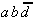 .
.
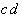 |
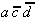 | 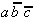 | 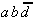 |
||
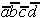 |
|||||
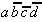 |
|||||
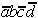 |
|||||
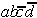 |
|||||
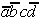 |
|||||
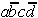 |
|||||
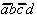 |
|||||
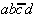 |
|||||
Table 2.5: Reduced Selection Table according to McCluskey.
In order to obtain a minimal Boolean function, as few as possible equivalent prime implicants should be used. With this requirement another reduction can be derived from Table 2.5. To realize the minterms m1 and m3 it is sufficient to consider the prime implicant 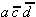 .
.
Therefore the final result for the (optimal) Boolean function is:
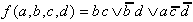 | . |
This result is equivalent to the one attained before.
Note:
The result determined with the Quine-McCluskey Method is a minimal Boolean function. But even in this case several equivalent solutions may exist.
The resulting function is presented as a DNF. Using the "De Morgan" Theorem it can be transformed into the desired form (NAND, NOR structure, etc.).
The advantage of the Quine-McCluskey Method is the precisely defined algorithm used to find the solution function. This opens the way to a simple e.g. programmed solution method.
An important disadvantage is that the function to be minimized has to exist as a canonical normal form (cDNF or cCNF). This means that an expansion of the function may be necessary. This also means that the McCluskey Table (prime term - minterm table) will get very large with a growing number of arguments.
Some newer methods are avoiding this restriction.
| Contents | Previous Chapter | Next Chapter |