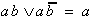2 Combinational Circuit Design

2.4 Circuit Simplification and Minimization

When a Boolean Function is realized as a canonical Normal Form (cDNF or cCNF) normally a large number of gates is necessary with a large number of gate inputs.

A simplified circuit implementation is therefore required. The following considerations indicate how such a reduction in circuit complexity can be achieved.

• Neighbouring fields of a Karnaugh Diagram differ in only one argument value, e.g. x_i = 0 and x_i = 1. Is the function value for those fields (the content of the field) equal, then the argument x_i is irrelevant (i.e. the value of these two fields does not depend on x_i). In the description of the function these two single fields can be replaced by one combined area, that covers both fields. This new combined field will be expressed without the argument x_i, i.e. the parameter x_i was eliminated.
  

• Combined fields of this kind can on their part now be combined to even larger fields (2 -> 4, 4 -> 8, etc.). With each doubling of the area another argument will be eliminated. The combination of 2ⁿ fields eliminates n arguments. Obviously this means that only a number of fields can be combined that can be expressed as a power of 2 (2ⁿ = 2,4,8,...).
  
  

Seen from the Boolean Algebra viewpoint this shows that the creation of larger areas means nothing else but repeatedly applying the equation

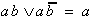. (2.7)

A Boolean function whose expression contains combined areas of this type does of course not present a canonical normal form anymore, but just a conjunctive (CNF) or disjunctive normal form (DNF).

Example:

The following example demonstrates on the K-Map how these combined fields can be formed:

Figure 2.21: Forming combined areas.

In this example the following 1-formations are possible:

• 4-Field m₀, m₁, m₄, m₅
• 2-Field m₁, m₃
• 2-Field m₄, m₆

Taking into consideration these field combinations, the function will be:

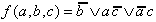(2-tier)

(2.8)

or, introducing the function XOR:

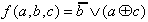(3-tier).

(2.9)

Obviously this example does not allow the formation of any 0-areas, so that only the realization as a cKNF is possible:

.

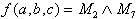(2.10)