| Figure 2.18: Sample Function. | 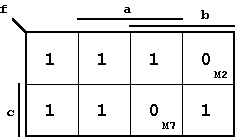 |
| Contents | Previous Chapter | Next Chapter |
As has been shown, an arbitrary Boolean Function can be realized using single-tier combinations of Mintems or Maxterms.
This approach to describe functions leads directly to the definition of so-called Canonical Forms
Definition:
Note:
The term "canonical" indicates that in this case the Boolean Function will be described in the most simple (and most elaborate) form. But in many cases simplifications are possible when describing functions (see below), so that the single terms will not be in the canonical forms anymore.
A cCNF as well as a cDNF are realized as two-tier (2-level) circuits. In case that in the first tier not all variables are used, the solution cannot be called "canonical" anymore.
In that case the corresponding Normal Forms are defined as:
Simplified both forms are also known as disjunctive and conjunctive form, respectively,
Furthermore the English literature has adopted the terms
Note: Using Maxterm Functions (Maxterms)
Experience shows that it seems somehow more difficult to use the Canonical Conjunctive Normal Form (cCNF). Therefore the basic procedure will be clarified in more detail using an example:
Karnaugh Diagram of a given arbitrary sample Boolean function:
| Figure 2.18: Sample Function. |  |
Obviously this Boolean function is totally described using six 1-fields and two 0-fields.
A Maxterm is described using a single 0-field, therefore it will be formed as a complete disjunction of all seven 1-fields. To describe the sample function two maxterms have to be used.
These two maxterms are the following terms M2 and M7:
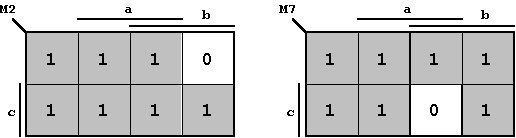
Figure 2.19: Maxterms to describe the Sample Function in Figure 2.18.
As can easily be seen, the overlay of these two maxterms will result in the sample Boolean function. It is clear that the maxterms have to be combined conjunctively, i.e. the cut-set has to be formed.
2.3.1 Example using functions:
Using the above definitions, the cDNF and the cKNF can be derived directly from the function's truth table.
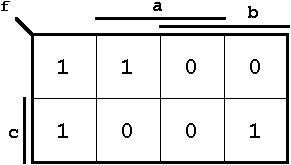
May the Boolean function f(a,b,c) be defined through the following truth table:
|
|
 |
a) Using the canonical Disjunctive Normal Form (cDNF):
In the canonical Disjunctive Normal Form fD all the conjunctions (AND-function) of the input variables a,b,c that have the result fD = 1 are combined disjunctively (OR-function).
In this example this means:
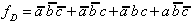 | . (2.1) |
Obviously only those rows (in the truth table) were considered for which f(a,b,c) is equal to '1'.
Using minterm notation equation 2.1 can be expressed as:
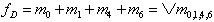 | . (2.2) |
b) Using the canonical Conjunctive Normal Form (cCNF):
In the canonical Conjunctive Normal Form fK all the disjunctions (OR-function) of the input variables a,b,c that have the result fK = 0 are combined conjunctively (AND-function).
In this example this means:
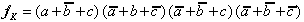 | . (2.3) |
Obviously only those rows (in the truth table) were considered for which f(a,b,c) is equal to '0'.
Using maxterm notation equation 2.3 can be expressed as:
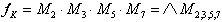 | . (2.4) |
Summary:
An arbitrary Boolean Function f(x1,...,xn) can always be expressed as cDNF (canonical Disjunctive Normal Form):
 | (2.5) |
or as
cCNF (canonical Conjunctive Normal Form):
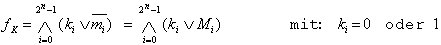 | , (2.6) |
with:
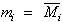
|
| with: mi = Minterm,
Mi = Maxterm. |
| Contents | Previous Chapter | Next Chapter |