2 Combinational Circuit Design

2.2 Minterms and Maxterms

There are some special Boolean Functions that - as can be seen just looking at the corresponding K-Maps - are built up in a very simple way. These are those functions that have only one single value '0' or '1'. By changing only this one function value these functions are transformed into the so-called 0-Function or 1-Function.

Therefore the function that contains only one '1' can be considered a minimal function, the one with only one '0' correspondingly a maximum function.

These special functions can be formed for an arbitrary number of arguments.

Definition:

Minterm Function: this function produces only a single '1'.
Maxterm Function: this function produces only a single '0'.

These functions are normal Boolean functions, but sometimes this fact is overlooked. In this case these functions are just referred to as Minterm and Maxterm, respectively.

In a K-Map these Boolean functions can be presented as follows:

a Minterm is a single field with an entry '1',
a Maxterm is a single field with an entry '0'.

As Minterm and Maxterm functions are determined by a single field, it would be sufficient for their characterization to indicate the type of term and the index of the distinguishing field. Common is the following abbreviated notation:

Minterm: m_i
Maxterm: M_i

The index i marks the field under consideration. It is determined by the values of the arguments (x,...,c,b,a).

Indexing Minterms and Maxterms:

Figure 2.15: Indexing the Minterm and Maxterm Functions.

Definition:

A Minterm m_i is a complete argument vector (a,b,c,...,x) for which a Boolean function f(a,b,c,...,x) delivers the value '1'.
A Maxterm M_i is a complete argument vector (a,b,c,...,x) for which a Boolean function f(a,b,c,...,x) delivers the value '0'.

Minterms and Maxterms are characterized by single fields and can therefore be described algebraically using:

a complete conjunction of all arguments (Minterm),
a complete disjunction of all arguments (Maxterm, as the complement of the 0-field).

Example:

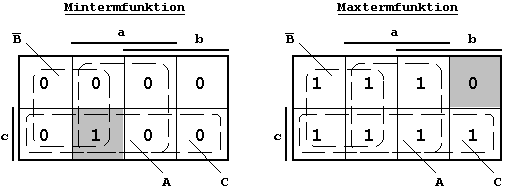
Figure 2.16: Production of Minterm and Maxterm Functions.

Using the abbreviations introduced above, the two functions in this example can be described algebraically as follows:

Minterm: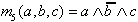
Maxterm: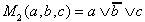

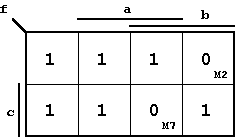
The example function can now be described with the aid of Minterms and Maxterms, respectively:

Karnaugh Diagram of the result function (see above):

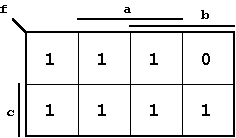
Figure 2.17: Example Function (Maxterm/Minterm description).

As can be seen from this K-Map, the Boolean function can be described using seven (7) Minterms or one (1) Maxterm.

7 Minterme: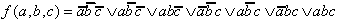
1 Maxterm: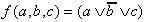

or, in short form:

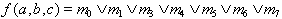
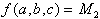Contents

Previous Chapter

Next Chapter