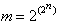 (1.3)
(1.3)
| Contents | Previous Chapter | Next Chapter |
As has been shown in the previous chapters, Boolean Function (also called switching functions) can be presented in manifold forms.
In principle a Boolean Functions is an assignment that can formally be defined using a mathematical expression. Besides this mathematical form another formal presentation exists using truth tables, i.e. using a tabular presentation of the functional relationship.
Assuming a Boolean Function f that has n arguments xi, the following generic truth table (value table) can be generated:
with: fi ∈ {0,1}
As can be seen, this table has 2n rows representing the function values that correspond to the 2n possible combinations of the variables x1,x2,...,xn.
Considering that in each row the function value can be 0 or 1, there are
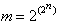 (1.3)
(1.3)
non-equivalent functions f(x1,x2,...,xn).
In the most simple case the Boolean Function depends on only one variable (so-called unary functions), so that
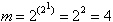
For the corresponding case of two variables (so-called binary functions)
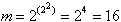
As can be seen, the number of possible Boolean Functions increases strongly with an increasing number of variables.
But from the following discussion it will be clear that only very few of these functions have nontrivial properties and are as such of importance for practical applications.
From the four possible Boolean Functions with only one variable (n=1) the most important one was already introduced, the Inverse Function, see above.
The following table gives a summary of all functions using truth tables, functional expressions, and Venn Diagrams. Whenever meaningful, the usual names and the digital circuit symbols are also included (following the two global standards).
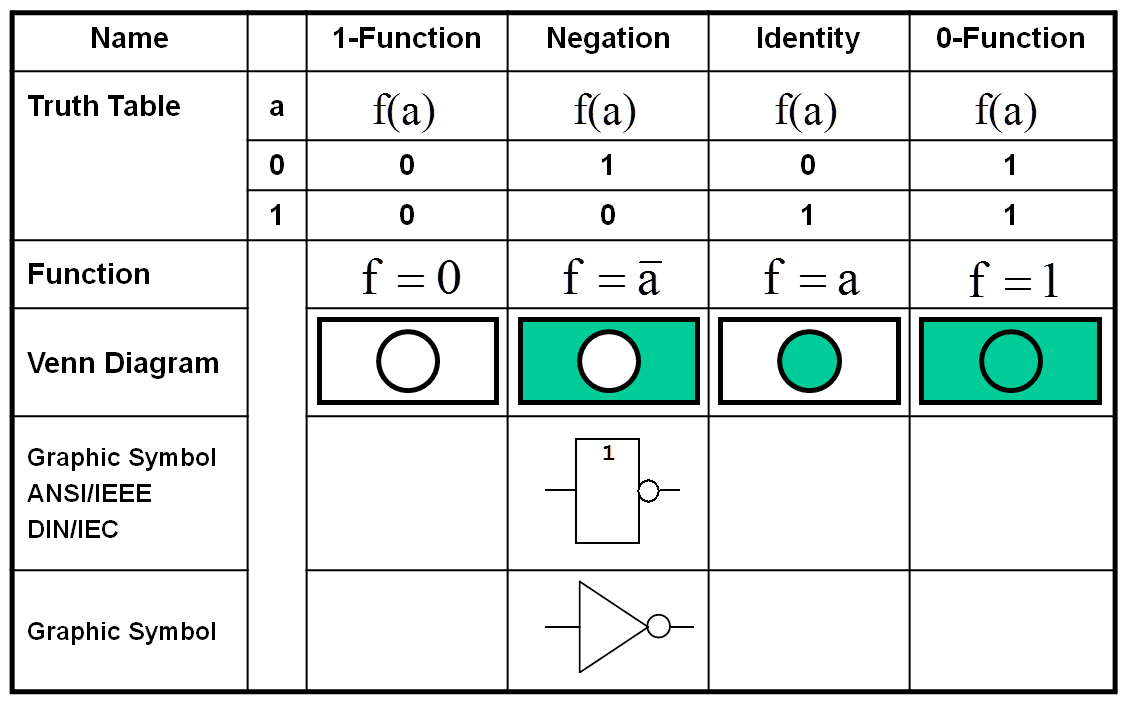
Following the presentation of the unary functions, the following four tables show all possible functions for n=2, the so-called binary functions:
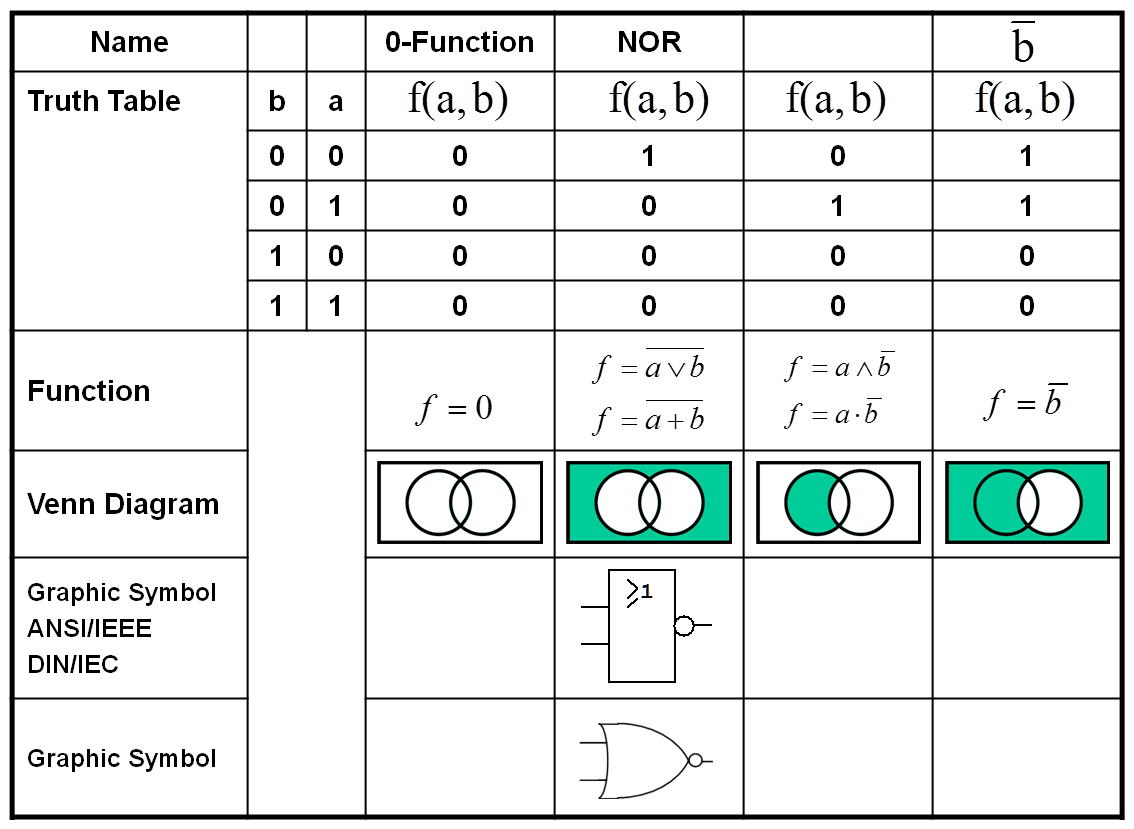
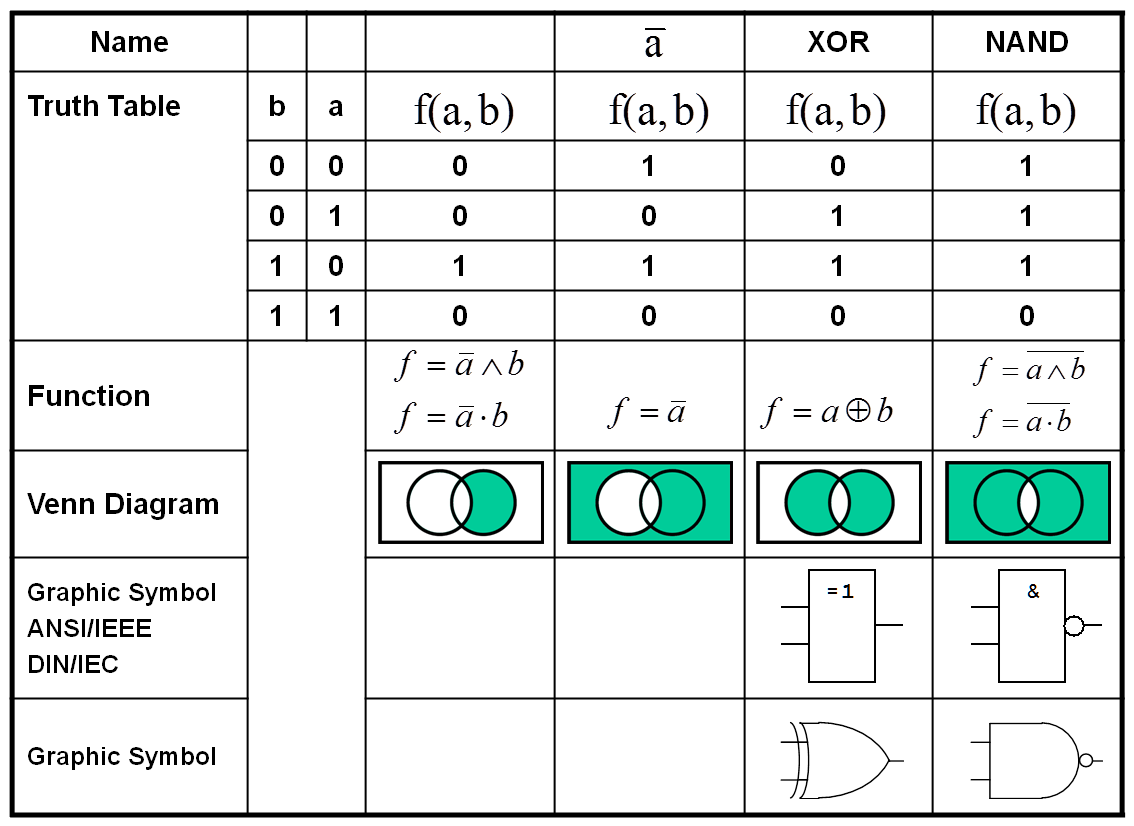
Figure 1.12: Binary Boolean Functions (Part 1 and 2).
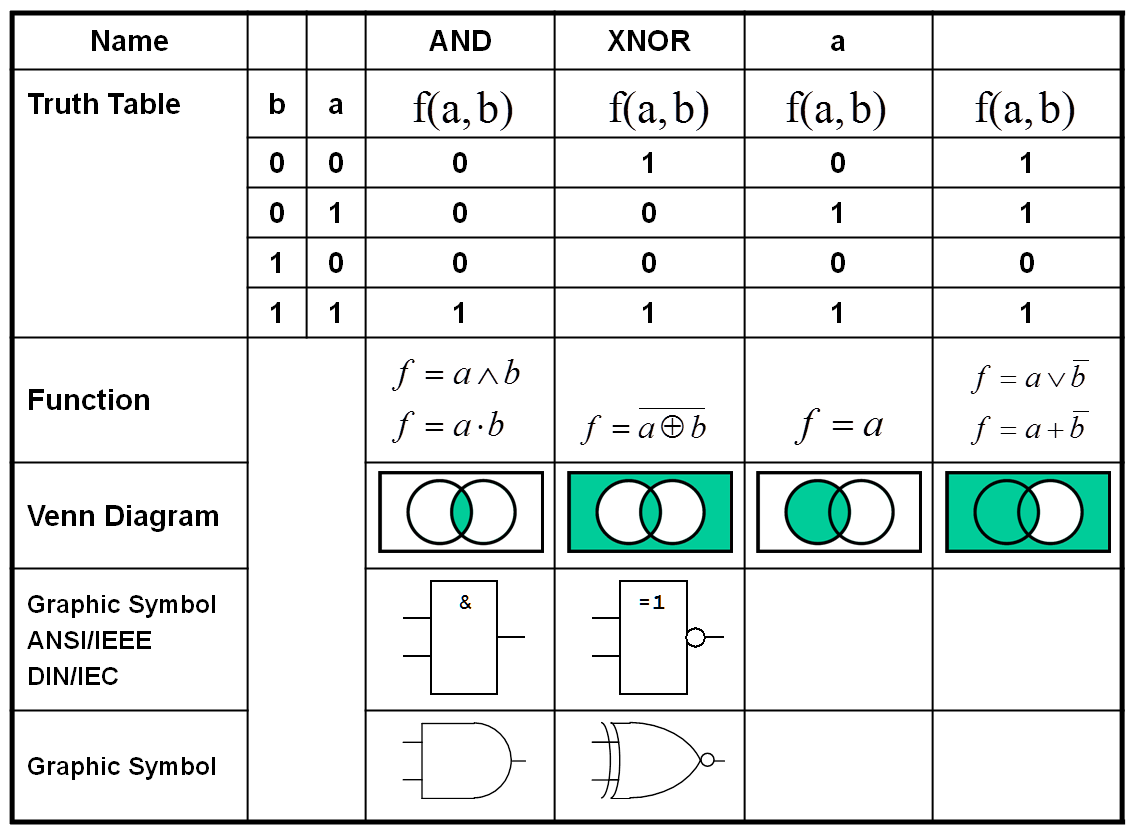
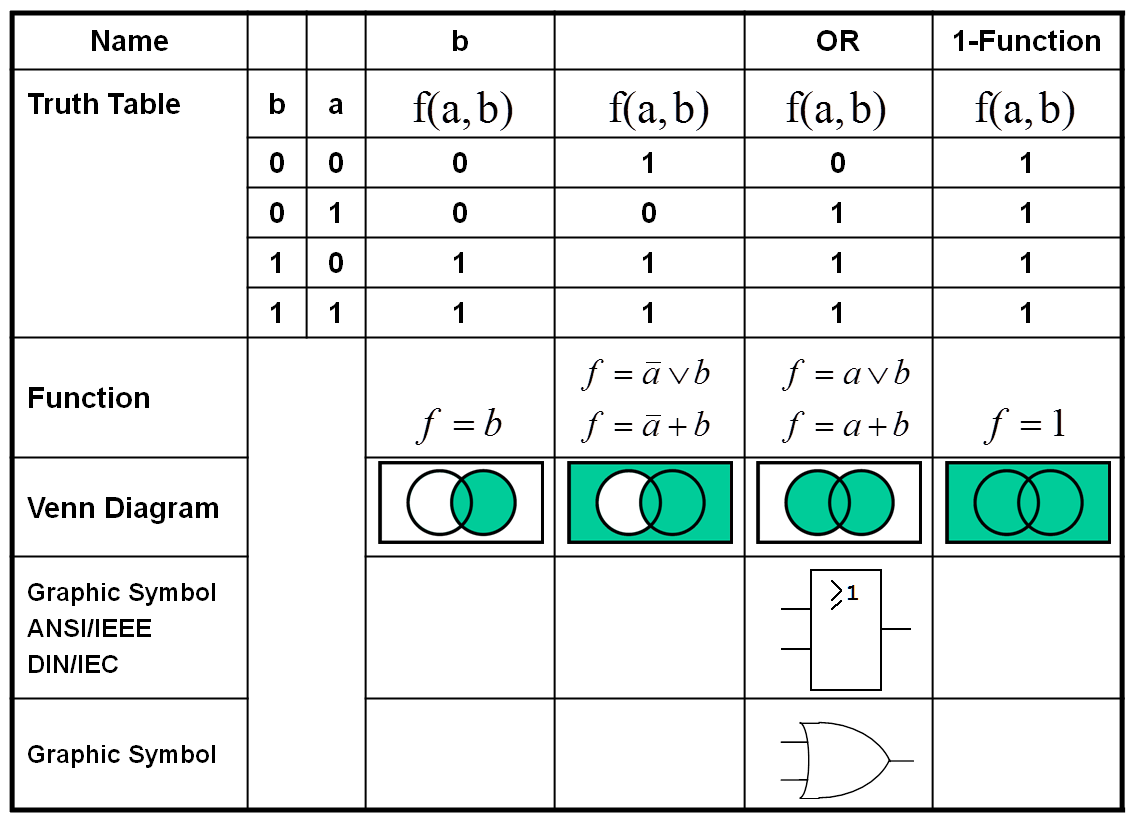
It has been shown that the number of all definable Boolean Functions will increase very strongly with increasing number of arguments. For n=3 there are already M=256 possible functions, most of them without importance.
In Digital Design a simplification has been accepted, limiting all applications, including those with functions n>=3, to the known functions with n=2 and their corresponding circuit symbols, but at the same time increasing the number of input variables (see below, AND or OR functions, respectively).
| Contents | Previous Chapter | Next Chapter |