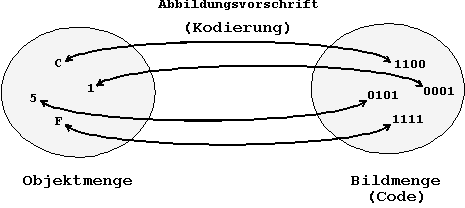
Abb.: 8.8: Kodierungsbeispiel:
Abbildung des Hexadezimalsystems in das Dualsystem.
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |
Mit dem Begriff "Kodierung"
wird eine Vorschrift bezeichnet, die einen vorgegebenen Zeichenvorrat
in einen neuen umwandelt. Es handelt sich um eine Abbildungsvorschrift,
durch die eine neue Elementenmenge erzeugt wird.
Der Begriff "Code"
hat die gleiche Bedeutung wie "Kodierung" (beide Begriffe
sind synonym). Darüberhinaus wird aber mit "Code"
auch der durch die Kodierung erzeugte, neue Zeichenvorrat gekennzeichnet,
d.h. die Menge der Elemente selbst.
Abb.: 8.8: Kodierungsbeispiel:
Abbildung des Hexadezimalsystems in das Dualsystem.
Wie an den bereits bekannten Kodierungsbeispielen
der polyadischen Zahlensysteme gesehen werden kann, sollten Kodierungen
bzw. Codes bestimmte Grundeigenschaften mitbringen.
Die wichtigste dieser Eigenschaften
ist die Eindeutigkeit der Zuordnung, d.h. daß jedes Element
der Objektmenge auf nur ein Element der Bildmenge abgebildet wird.
Für die Rückabbildung von der Bildmenge in die Objektmenge
braucht diese Eigenschaft nicht zu bestehen, die Forderung nach
einer umkehrbar eindeutigen Abbildung wird nicht gestellt.
Auf die umkehrbare Eindeutigkeit
wird oftmals bewußt verzichtet, um eine Optimierung zu erhalten.
Dies bedeutet z.B., daß mehrere Elemente der Objektmenge
auf ein einziges Element der Bildmenge abgebildet werden können.
Zur vollständigen Informationsverarbeitung
reicht die Kodierung rein numerischer Daten nicht aus. Die Kodierung
muß auch alphabetische Information erfassen.
Die Codes können daher in zwei Gruppen unterteilt werden:
Die alphanumerischen Codes dienen
zur Darstellung von numerischer und nicht-numerischer Information
(dazu gehören das Alphabet, Sonderzeichen wie '.' oder ','
und auch nicht druckbare Spezialzeichen, s.u.).
Es bestehen weitere Möglichkeiten,
Codes zu charakterisieren. Codes können z.B. klassifiziert
werden in
Einige dieser (sich nicht gegenseitig
ausschließenden) Charakteristika sollen im folgenden näher
erläutert werden.
Stellenzahl n:
Binäre Codes (als Bildmenge)
werden als Bitkombinationen realisiert. Die Stellenzahl n des
Codes entspricht der Anzahl von Bits, die für die Kodierung
vorgesehen ist. Die Zahl n definiert damit die Informationsbreite
des Codes.
Codegewicht:
Als Gewicht g eines Codewortes
wird die Anzahl der Stellen mit dem Wert "1" bezeichnet
(Beispiel: g(0101) = 2, g(0000) = 0).
Gleichmäßigkeit:
Ein Code wird als gleichmäßig
bezeichnet, wenn die Stellenzahl n für alle Werte gleichgroß
(konstant) ist.
Nachrichtenmenge M:
Mit Hilfe dieser Stellenzahl m ergibt
sich die maximal darstellbare Nachrichtenmenge, d.h. die maximale
Zahl unterscheidbarer Codes, bei einem Binärcode zu:
| M = 2m | . | (8.29) |
Redundanz R:
Ist die darzustellende Anzahl von Codes kleiner als die maximale Nachrichtenmenge M, so ergibt sich eine Redundanz: es existieren mehr Bitkombinationen als zur Code-Realisierung notwendig sind.
Die Redundanz beschreibt also die
Differenz zwischen der realisierbaren Nachrichtenmenge M
und der tatsächlich realisierten Nachrichtenmenge N.
Mathematisch ausgedrückt wird die Redundanz als Bit-Redundanz,
d.h. als die Differenz zwischen der Stellenzahl m und der
effektiv notwendigen Bitanzahl n.
Für n gilt damit die Beziehung:
| N = 2n | . | (8.30) |
Aus Gl. 8.29 und Gl. 8.30 folgt:
| m = ld(M), n = ld(N) | (8.31) |
| mit: ld = Logarithmus zur Basis 2. |
Damit kann die Redundanz definiert werden als:
| R = ld(M) ld(N) | ; | (8.32) |
| R = m ld(N) [Bits] |
Da die Zahl N nicht notwendigerweise eine ganzzahlige Potenz von 2 sein muß, ergibt sich für die Redundanz im allgemeinen eine gebrochene Zahl.
Redundanz kann verwendet werden,
um fehlererkennende bzw. fehlerkorrigierende Codes
aufzubauen.
Beispiel 8.16: Redundanz eines dekadischen 4-Bit-Codes (BCD, s.u.)
| R | m ld(N) | , | |
| 4 - ld(10) | |||
| 4 - 3,32 = 0,68 | |||
| R | 0,7 Bits | . |
Die Redundanz beträgt 0,7 Bits;
zur Realisierung von 10 Codeworten wären (theoretisch) 3,3
Bits ausreichend.
Vollständigkeit:
Werden alle möglichen Bitkombinationen
genutzt (N = M), wird der Code als vollständig
bezeichnet. Ein vollständiger Code ist nicht redundant:
Hammingabstand (Hamming-Distanz):
Der Hammingabstand h gibt die Anzahl der Stellen an, in denen sich zwei beliebige Worte eines Codes unterscheiden.
Für zwei Codeworte a = (a1,a2,...,an)
und b = (b1,b2...,bn)
kann h mit Hilfe der XOR-Funktion bestimmt werden:
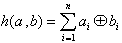 | (8.33) |
(
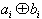ist hierbei als ganze Zahl aufzufassen)
| oder: | 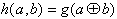 | . | (8.34) |
Stetigkeit:
Bei einem stetigen Code ist der Hammingabstand konstant über den gesamten Code.
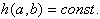 | für beliebige a,b mit ab. |
Einschrittigkeit:
Gilt für einen stetigen Code,
daß die Hammingdistanz h = 1 ist, wird der Code
als einschrittig bezeichnet. Dies bedeutet, daß zwischen
zwei beliebig gewählten benachbarten Codeworten sich nur
ein einziger Bitwert ändert.
Code-Symmetrie:
Ein Code wird als symmetrisch bezeichnet,
wenn die möglichen Codeworte symmetrisch um eine imaginäre
Symmetrieachse (einen bestimmten Codewert) verteilt sind. Bei
den tetradischen BCD-Codes (s.u.) ist eine Symmetrie bezüglich
der Binärzahl 10002
wichtig, da in diesem Fall das Neunerkomplement besonders einfach
gebildet werden kann. Arithmetische Operationen werden dadurch
erleichtert.
Lexikografische Codes:
Codes werden als lexikografisch angeordnet bezeichnet, wenn die Codeworte in der Reihenfolge ihrer Dualwerte geordnet sind.
Lexikografisch sind z.B. der nBCD-Code
und der Aiken-Code, nicht lexikografisch sind die Gray- und Glixon-Codes
(s.u).
Selbstkomplementierende Codes:
Bei selbstkomplementierenden Codes
entspricht das Neunerkomplement einer Dezimalzahl dem Einerkomplement
der zugehörigen Dualzahl.
Die in Kap. 8.5.1 vorgenommene
Einteilung in numerische und alphanumerische Codes kann weiter
verfeinert werden. Die numerischen Codes können ihrerseits
unterteilt werden:
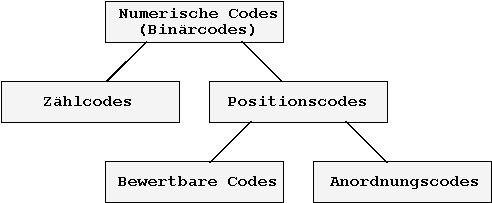
Abb. 8.9: Klassifizierung der numerischen Codes.
Alle hier dargestellten Codes können weiterhin klassifiziert werden in:
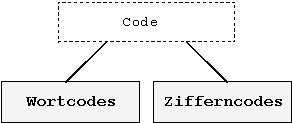
Abb.: 8.10: Wortcodes und Zifferncodes.
Die Wortcodes nehmen hierbei
eine wortweise Kodierung vor, wie sie z.B. von den Dualzahlen
her bereits bekannt ist.
Im Gegensatz dazu wird bei den Zifferncodes
die Dezimalzahl ziffernweise kodiert.
Zifferncodes haben den Vorteil einer
einfacheren Kodierung, der allerdings mit einer größeren
Redundanz erkauft wird: es existieren ungenutzte Bitkombinationen
(nicht realisierte Codes).
Bei den Positioncodes ist die Position
der einzelnen Bits von Bedeutung, die allerdings nicht wie bei
den polyadischen Zahlensystemen einer linearen Reihenfolge gehorchen
muß.
Positionscodes können in zwei Gruppen unterteilt werden:
Die bewertbaren Codes folgen im Prinzip dem Bildungsgesetz Gl. 8.1:
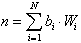 | . | (8.1) |
Die Gewichte Wi definieren diesen Codetyp als bewertbar (bzw. "wägbar").
Zu den bewertbaren Codes gehört ein Teil der unter dem Namen "BCD-Zahlen" zusammengefaßten Systeme. BCD-Zahlen entstehen durch ziffernweise Kodierung von Dezimalzahlen; im Gegensatz zur Kodierung als Dualzahl wird in diesem Fall also die Dezimalzahl zunächst in ihre einzelnen Dekaden (Koeffizienten) zerlegt, die dann einzeln kodiert werden.
Die Bezeichnung "BCD" soll
diesen Vorgang zum Ausdruck bringen:
Das wichtigste BCD-Zahlensystem zieht
zur Kodierung das Dualsystem heran und wird deshalb als nBCD-System
bezeichnet:
Eine vorgegebene Dezimalzahl d3d2d1d0
wird also zur Kodierung als nBCD-Zahl ziffernweise in das Dualsystem
konvertiert:
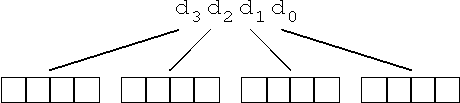
Abb. 8.11: Wandlung einer Dezimalzahl in eine BCD-Zahl
Beispiel 8.17:
In dieser Darstellung wurde bereits
angenommen, daß die BCD-Zahl mit 4 Bits dargestellt wird.
Dies ist die minimal notwendige Stellenzahl, da hiermit 24 = 16
unterschiedliche Zahlen kodiert werden können. Offensichtlich
besteht ein Überschuß an Kodierungsmöglichkeit
(s.o. "Redundanz"), da nur 10 Zahlenwerte vorliegen
(0 - 9). Die nicht genutzten Codes sind die sogenannten
Pseudotetraden (Pseudodekaden, Pseudodezimalen) des BCD-Codes
(s. Kap. 2).
Die Redundanz des BCD-Codes im Vergleich
zum reinen Binärcode zeigt sich auch im direkten Vergleich
der Wertebereiche die vorliegen, wenn die gleiche Anzahl von Binärstellen
vorausgesetzt wird.
Beispiel 8.18: Vergleich einer 16-stelligen Binär- und BCD-Zahl
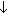
BCD-Zahl (4 Dekaden, Tetraden)
Für die Wertebereiche ergibt sich in diesen beiden Fällen:
| Binärzahl (16 Bits): | 0 - 65535 |
| BCD-Zahl (4 Dekaden): | 0 - 9999 |
In der folgenden Tabelle werden einige
bewertbare 4-Bit-BCD-Codes (Tetradencodes) zusammengefaßt:
| Code-Name | ||||||
| Gewicht | ||||||
Tab. 8.10 4-Bit-BCD-Codes
Beispiel 8.19: (569)10 = (0101 0110 1010)7421
Der Aiken-Code (2421-Code) hat als besondere Eigenschaft die Selbstkomplement-Bildung; Neunerkomplement des Dezimalwertes und Einerkomplement des Dualwertes sind identisch:
Tab. 8.11: Beispiel für Selbstkomplementierung.
Ein weiterer stellenbewerteter aber
nicht selbstkomplementärer 2421-Code, der dem Aiken-Code
sehr ähnlich ist, wird in Tab. 8.14 wiedergegeben.
Die Bildung von bewertbaren BCD-Codes
kann auch mit mehr als 4 Bits vorgenommen werden. Einige
dieser nichttetradischen Codes werden in nachfolgender Liste wiedergegeben:
| Code-Name | Code | Code | ||
| Gewicht | ||||
Tab. 8.12: Nichttetradische BCD-Codes
2-aus-5-Code und Biquinär-Code:
Von den hier wiedergegebenen nichttetradischen
Codes enthalten sowohl beim 2-aus-5- als auch beim Biquinär-Code
sämtliche Codeworte genau 2 "1"-Werte. Diese regelmäßige
Anordnung macht die automatische Fehlererkennung besonders einfach.
Beim Biquinär-Code kommt hinzu,
daß diese beiden Einsen jeweils auf eine linke und eine
rechte Gruppe verteilt werden, wodurch selbst Zweibitfehler zum
Teil erkannt werden können.
51111-Code:
Der 51111-Code ist wie der Aiken-Code selbstkomplementierend (s.o.).
Im Gegensatz zu den Positionscodes
haben die Anordnungscodes kein einfaches mathematisches Bildungsgesetz
und werden deshalb häufig direkt über die Codetabelle
definiert.
Sie zeichnen sich aber durch besondere
Eigenschaften aus, wie Symmetrie, Einschrittigkeit, einfache Realisierung,
etc..
Zu den wichtigsten Anordnungscodes
gehören die Gray-Codes, die als dekadische 4-Bit-Codes
vorliegen und in erweiterter Form alle 16 möglichen 4-Bit-Codewörter
nutzen.
Mathematisch kann der Gray-Code mit
Hilfe der XOR-Funktion gebildet werden (s. Kap. 2), einfacher
ist seine Darstellung mit Hilfe einer grafischen Bildungsmethode
(siehe Abb. 8.12). Ausgehend von einer 0/1-Kombination wird durch
wiederholtes Spiegeln der Ausgangsinformation und Hinzufügen
von 0/1-Werten der vollständige Code aufgebaut:
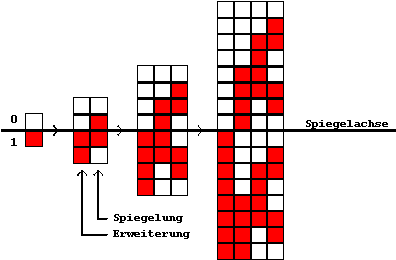
Abb. 8.12: Bildung des Gray-Codes durch Spiegelung und Bit-Erweiterung.
Auf Grund dieses grafischen Bildungsgesetzes
wird dieser Code auch als binärer Reflexcode (BRC)
bezeichnet.
Der so gebildete Gray-Code ist vollständig
und hat als weitere Grundeigenschaft die Einschrittigkeit, die
auch aus dem KV-Diagramm entnommen werden kann:
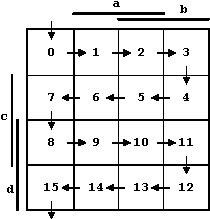
Abb. 8.13: KV-Diagramm des vollständigen Gray-Codes.
Eine andere Darstellungsform des
Codes bedient sich eines sogenannten Codelineals, in dem die einzelnen
Bit-Positionen farblich gekennzeichnet werden:
Abb. 8.14: Codelineal des Gray-Codes.
Der hier gezeigte Code kann auch auf eine Dekade verkürzt werden, um BCD-Zahlen zu realisieren. Wie am obigen Codelineal gesehen werden kann, geht allerdings bei dieser Verkürzung die Einschrittigkeit beim Übergang von 910 auf 010 verloren; der neue Code ist nicht mehr zyklisch (bzgl. modulo 10).
Abhilfe schafft eine kleine Modifikation
des Codes für die Zahl 910,
wodurch die Einschrittigkeit wiederhergestellt wird. Der resultierende
Code wird als Glixon-Code bezeichnet.
Abb. 8.15: Gray- und Glixon-Codes.
Die Einschrittigkeit macht den Gray- bzw. Glixon-Code besonders wichtig. Insbesondere bei meßtechnischen Anwendungen sind einschrittige Codes notwendig, um inkorrekte Meßergebnisse oder fehlerhafte Informationswandlungen (z.B. bei A/D-Umsetzung) zu vermeiden.
Der Vergleich mit dem Dualsystem zeigt dies besonders deutlich.
Zum Messen von Längen können Meßlineale eingesetzt werden, die im Prinzip den bereits eingeführten Codelinealen entsprechen. Winkel können mit Hilfe von ähnlich aufgebauten Winkelgebern bestimmt werden.
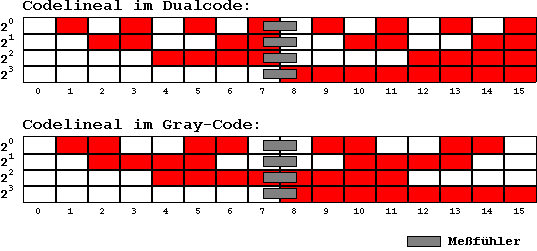
Abb. 8.16: Messung mit dem Codelineal
Bei Messung mit dem dualcodierten
Lineal (Abb. 8.16 oben) ist der Übergang vom Wert 7 auf den
Wert 8 besonders kritisch; alle Binärstellen ändern
sich (h = 4). Wird die Abtastung z.B. mit einem optischen
Sensor vorgenommen, kann nicht garantiert werden, daß alle
Bitpositionen zur exakt gleichen Zeit wechseln. Schon auf Grund
einer kleinen Leseverzögerung kann ein falscher Wert (z.B.
"0") ermittelt werden.
Beim Gray-Code-Lineal (Abb. 8.16
unten) kann diese Fehlersituation nicht auftreten. Selbst bei
zeitverzögerter Abtastung einzelner Bits ergibt sich kein
Codesprung, so daß kein falscher Zwischenwert ausgegeben
werden kann.
In Meßinstrumenten dieser Art
werden also grundsätzlich einschrittige Codes realisiert.
Weitere wichtige Anordnungscodes werden in der nachfolgenden Tabelle wiedergegeben:
Exezeß-3 | Craig | |||
Tab.8.13: Wichtige Tetraden- und Pentaden-Codes
Exzeß-3-Code (Stibitz-Code):
Der Exzeß-3-Code entsteht aus
dem nBCD-8421-Code durch Addition des Zahlenwertes "3"
(daher seine Bezeichnung). Dieser Code ist symmetrisch (vgl. Tab.
8.14) und enthält nicht die 0000- und 1111-Worte, was für
nachrichtentechnische Zwecke von Vorteil ist (diese Bitkombinationen
können bei technischem Fehlverhalten leicht auftreten, sie
stellen in diesem Fall aber Pseudotetraden dar). Der Exzeß-3-Code
ist außerdem selbstkomplementierend (s.o. Aiken-Code).
Libaw-Craig-Code:
Der Libaw-Craig-Code ist einschrittig und stetig; außerdem ist bei diesem Code die Bildung des Zehnerkomplements besonders einfach: der Dualcode wird in umgekehrter Richtung gelesen.
Zusammenfassung:
Zusammenfassend sollen die wichtigsten
hier behandelten Codes in ihrer Zuordnung zum vollständigen
4-Bit-Dualcode aufgezeigt werden.
Diese Form der Anordnung erlaubt
es in besonders einfacher Form, wichtige Grundeigenschaften der
Codes zu ermitteln (Symmetrie, lexikografische Anordnung, etc.).
(nBCD) | unsym. | (16 bit) | |||||
Tab. 8.14: Wichtige 4-Bit-BCD-Codes
Bei den hier dargestellen 4-Bit-Codes
handelt es sich um die bekanntesten. Anspruch auf Vollständigkeit
kann schon deshalb nicht erhoben werden, weil die Zahl der theoretisch
möglichen tetradischen Verschlüsselungen äußerst
groß ist:
Bei einer Stellenzahl von 4 Bits
gibt es für die Kodierung dezimaler Zahlen (mit 6 Pseudotetraden)
insgesamt
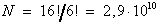
Kombinationsmöglichkeiten. Die meisten dieser fast 3·1010 definierbaren Codes haben natürlich keine technische Bedeutung.
Bei der Durchführung arithmetischer
Operationen zeigen die verschiedenen BCD-Codes recht unterschiedliches
Verhalten. Insbesondere müssen die Pseudotetraden berücksichtigt
werden, d.h. es müssen Korrekturen an den (Zwischen-)Ergebnissen
durchgeführt werden.
Die notwendigen Anpassungen z.B.
bei einer Addition sind besonders einfach beim nBCD-Code sowie
beim Exzeß-3- und Aiken-Code, die beide in einer engen Beziehung
zueinander stehen:
Beispiel 8.20: Addition im nBCD-Code
mit Übertrag mit Pseudotetrade
__________________ __________________
810 1000 710 0111
+ 910 1001 + 610 0110
__________________ __________________
= 1710 0001 0001 = 1310 1101
+ 0110 + 0110 <-- Korrektur (+6)
____________ ___________
0001 0111 0001 0011 <-- Endergebnis
Beispiel 8.21:
Addition im Exzeß-3-Code
mit Übertrag ohne Übertrag
(Pseudotetrade)
__________________ __________________
410 0111 310 0110
+ 910 1100 + 410 0111
__________________ __________________
= 1310 1 0011 = 710 1101
+ 0011 0011 - 0011 <-- Korrektur (±3)
____________ ___________
0100 0110 1010 <-- Endergebnis
Die Zählcodes sind sehr einfach aufgebaut. Um einen gegebenen Zahlenwert darzustellen, wird die entsprechende Anzahl von Einsen angegeben. Führende Bitpositionen werden durch Nullen aufgefüllt:
. . | . . |
Tab. 8.15: Binäre Codierung im Zählcode
Auch Zählcodes können als Wort- bzw- Zifferncode definiert werden.
Beim Wortcode wird die Stellenzahl
bestimmt durch den größten darzustellenden Zahlenwert.
Beim Zifferncode wird jede einzelne Dezimalzahl in Form einer BCD-Zahl binär codiert.
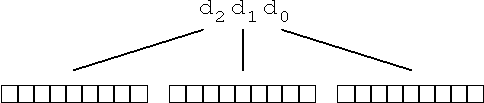
Abb. 8.17: Wandlung einer Dezimalzahl in eine zählcodierte BCD-Zahl
Für jede Dezimalstelle sind also neun Bits notwendig:
. . | . . |
Tab. 8.16: Codierung von BCD-Zahlen im Zählcode
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |