
Abb. 6.4: Vorwärts-Rückwärtszähler (Modulo-4).
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |
Eine wichtige Teilgruppe der synchronen Schaltwerke stellen die sogenannten Steuerwerke dar.
Ihre Behandlung basiert auf der Theorie
der endlichen Automaten (Zustandsmaschine, engl. finite
state machine, FSM).
In den Steuerwerken wird die Logik
des Verknüpfungsnetzes durch einen Speicher realisiert. Steuerwerke
sind auf Grund dieses Aufbaus sehr einfach gestaltet und leicht
modifizierbar.
6.2.1 Mealy- und Moore-Automaten
Bisher sind nur die Zustände
der Schaltwerke behandelt worden, über die Ausgabe ist noch
keine Festlegung erfolgt.
Als Beispiel soll der bereits behandelte Modulo-4-Zähler durch Einführung eines Steuereingangs "Vor/Rück" erweitert werden.
Mit diesem Eingangssignal kann die Zählrichtung definiert werden: Liegt der Eingang auf '1', wird aufwärts, andernfalls wird abwärts gezählt.

Abb. 6.4: Vorwärts-Rückwärtszähler (Modulo-4).
Der Zähler soll derart realisiert
werden, daß folgende Zustandskodierung erfüllt wird:
Bei dieser als "einschrittig"
bezeichneten Kodierung ändert sich mit jedem Übergang
nur ein einziges Bit. Eine derartige Kodierung hat den Vorteil,
daß Funktions-Hazards nicht auftreten können.
Unter Annahme dieser Kodierung ergibt
sich für das Zustandsdiagramm dieses Zählers:
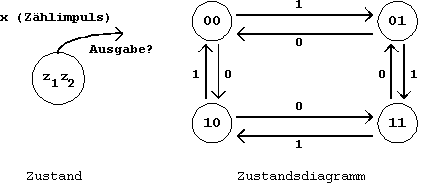
Abb. 6.5: Zustandsdiagramm des Modulo-4-Zählers.
Für den hier gezeigten Automaten
sind jetzt in geeigneter Form die Begriffe "aktueller
Zustand" und "Ausgabe" zu definieren.
Definition des aktuellen Zustandes:
Nur bei den synchronen Steuerwerken
existieren zwei Alternativen für die Beschreibung des aktuellen
Zustandes: es können sowohl die Rückkopplungsausgänge
als auch die Rückkopplungseingänge zu diesem Zweck herangezogen
werden.
Offensichtlich ist es sinnvoller,
dafür die stabilen Ausgangswerte des Registers zu nutzen,
in diesem Fall also z1 und z2.
Da nur in diesem stabilen Zustand
eine Änderung der externen Eingabe x zulässig ist, ändern
sich auch direkt die Ausgänge v1 und v2.
Der neue Zählzustand wird mit der Vorderflanke des Taktimpulses
übernommen.
Definition der Ausgabe:
Für die Wahl der Ausgabe bieten
sich zwei Möglichkeiten an:
Es können entweder die Ausgänge
yi
des Verknüpfungsnetzes VN1
oder die entsprechenden Ausgänge von VN2
genutzt werden.
Sicherlich zweckmäßiger
ist eine Ausgabe über VN2,
da in diesem Fall die Ausgabewerte nicht direkt von einem Wechsel
am Eingang x beeinflußt werden. Die Ausgangswerte hängen
lediglich von dem augenblicklichen Zustand ab, der durch z1
und z2
bestimmt wird.
Das in dieser Form betriebene Steuerwerk
wird als Moore-Automat bezeichnet. Da in diesem Fall die
Ausgabe vollständig durch den aktuellen Zustand beschrieben
wird, ergibt sich für diesen Automaten das folgende Zustandsdiagramm:
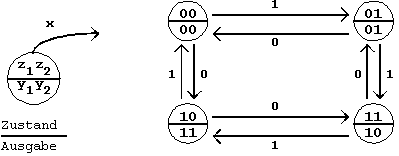
Abb. 6.6: Zustandsdiagramm im Moore-Format.
Die Zustandsdefinition wurde in dieser Darstellung modifiziert, um die direkte Anbindung der Ausgabe an den aktuellen Zustand aufzuzeigen.
Wird im Gegensatz zur obigen Lösung
eine Ausgabe über VN1
gewählt, so wird diese von einer Eingangsänderung (x)
unmittelbar beeinflußt.
In diesem Fall wird das entstandene
Steuerwerk als Mealy-Automat bezeichnet.
Das zugehörige Zustandsdiagramm
reflektiert den veränderten Sachverhalt:

Abb. 6.7: Zustandsdiagramm im Mealy-Format.
Auch in diesem Fall wurde die Zustandsdefinition
so gewählt, daß die Abhängigkeit der Ausgabe von
der Eingabe sichtbar wird ("x/y1y2";
y1y2
ändern sich mit der Eingangsvariablen x).
Der Unterschied zur oben gezeigten
Moore-Darstellung wird sofort sichtbar, wenn das Verhältnis
von Zustands- zu Ausgangsänderung untersucht wird.
Beispiel:
Der Automat (Zähler) befinde
sich in Zustand '01'. Wird jetzt der Eingang "x" auf
'1' gelegt, ergibt sich folgendes:
Der Unterschied zwischen den eingeführten
Automaten kann also zusammenfassend beschrieben werden:
Moore-Notation: Bei einem Schaltwerk vom Moore-Typ wird die Ausgabe nur direkt vom aktuellen Zustand bestimmt. Eine Änderung der externen Eingabe hat erst über die Zustandsänderung einen Einfluß auf die Ausgabe. Die Ausgabe erfolgt synchron.
Mealy-Notation: Bei einem
Schaltwerk vom Mealy-Typ hängt die Ausgabe sowohl vom aktuellen
Zustand als auch direkt von der externen Eingabe ab. Die Ausgabe
erfolgt asynchron.
Vergleicht man die entsprechenden Zustandsdiagramme, so kann außerdem der Unterschied der Automaten dadurch charakterisiert werden, daß bei einem Mealy-Automaten die Ausgabe gegenüber dem Zustandswechsel und damit gegenüber einem Moore-Automaten vorauseilt.
Hinweis:
Da trotz der einschrittigen Zustandsänderung
sowohl im Moore- als auch im Mealy-Betrieb der Zählerstand
als Binärwert ausgegeben werden soll, müssen die für
die Ausgabe verantwortlichen Verknüpfungsnetze VN1
bzw. VN2
die erforderliche Ausgabefunktion erfüllen:
Tab. 6.1: Definition der Ausgabefunktion.
Hinweis:
Diese Ausgabe über ein Verknüfungsnetz (VN1) ist wegen der direkten Abhängigkeit von der externen Eingabe für eine Mealy-Ausgabe immer erforderlich.
6.2.2 Mealy- und Moore-Automaten:
Prinzipschaltungen
Das hier am Beispiel des Vorwärts-Rückwärtszähler
eingeführte Automatenmodell kann jetzt in verallgemeinerter
Form dargestellt werden.
Moore- und Mealy-Automaten können
durch die folgenden Prinzipschaltungen beschrieben werden:
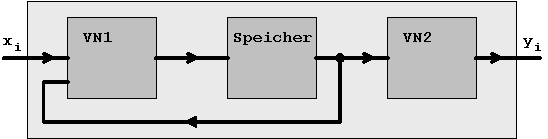
Abb. 6.8: Moore-Automat
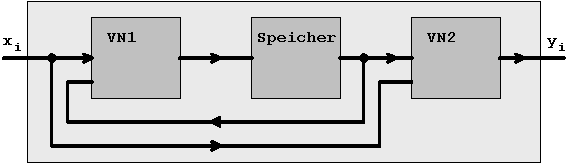
Abb. 6.9: Mealy-Automat
6.2.3 Speicherrealisierung von Steuerwerken
Wie bereits gezeigt wurde, ist es
möglich, die Realisierung von logischen Funktionen mit Hilfe
von Speicherbausteinen durchzuführen. Bei diesem Verfahren
wird die Wertetabelle der darzustellenden Booleschen Funktion
direkt im Speicher abgelegt.
In ähnlicher Form kann natürlich
auch der Aufbau eines Steuerwerkes vorgenommen werden, indem das
für die logische Funktion verantwortliche Verknüpfungsnetz
VN durch eine Speicherrealisierung ersetzt wird.
Der Speicher soll für diese Anwendung als RAM-Speicher (random access memory) ausgelegt sein, d.h. es soll ein wahlfreier Zugriff auf die individuellen Speicherzellen möglich sein. Jede einzelne Speicherposition ist also über eine eindeutige Addresse "ansprechbar", der Inhalt des Speichers wird auf diese Weise zugänglich.
| Abb. 6.10: Speicherorganisation | 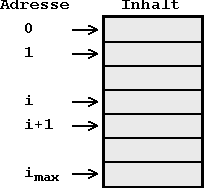
|
Beispiel:
Ein aus 32 Speicherzellen aufgebauter Speicher, der unter jeder Adresse zwei Bits ablegen kann:
|
|
| |||||
Tab. 6.2: Definition der Speicherzellen.
Um im Speicher eine Boolesche Funktion zu verwirklichen, werden jetzt die Funktionsargumente als Speicheradressen interpretiert. Der Inhalt der Speicherzellen repräsentiert den entsprechenden Funktionswert.
Handelt es sich also um eine Funktion mit n Argumenten, sind insgesamt 2n Speicherstellen notwendig. Für jede einzelne Speicherzelle ist eine Informationsbreite von einem Bit notwendig (für jede Argumentenkombination kann der Funktionswert nur '0' oder '1' sein).
Sollen mehrere Funktionen, die von
den gleichen Argumenten abhängen, im Speicher realisiert
werden, ist für jede Funktion also eine Informationseinheit
von einem Bit nötig.
Beispiel:
Zwei Funktionen f(a,b,c,d,e) und
g(a,b,c,d,e) sollen gemeinsam in einem Speicher realisiert werden.
Die Gesamtkapazität des notwendigen Speichers ist also 32 * 2 Speicherzellen (Bit):
| Tab. 6.3: Speicherrealisierung zweier Funktionen. | 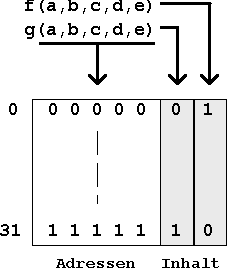
|
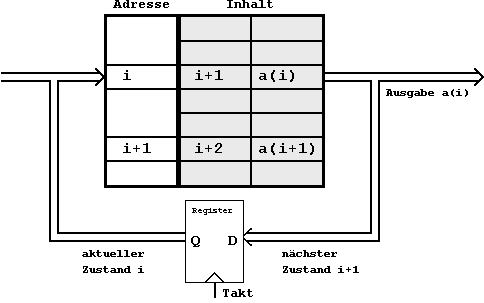
Abb. 6.11: Speicherrealisierung eines Automaten.
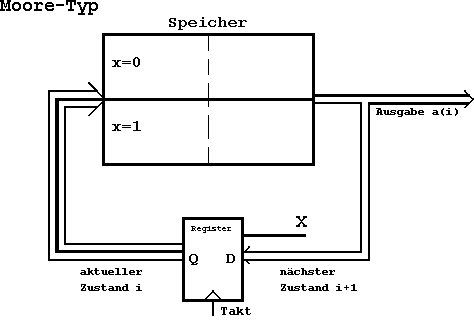
Abb. 6.12: Speicherrealisierung eines Moore-Automaten.
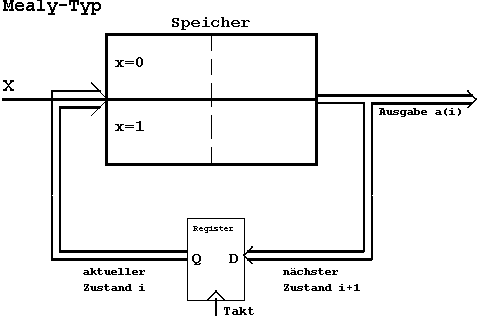
Abb. 6.13: Speicherrealisierung eines Mealy-Automaten.
6.2.4 Anwendung von Mikroprogramm-Steuerwerken
Eine wichtige Anwendung speicherrealisierter
Steuerwerke bildet der Aufbau von Mikroprogramm-Steuerwerken zur
Befehlssteuerung in modernen Mikroprozessoren.
Ein vorgegebener Mikroprozessor-Befehl
wird in diesem Fall zerlegt in eine Folge von sogenannten Mikrobefehlen.
Die entsprechende Sequenz wird in einem Mikroprogramm-Speicher
abgelegt.
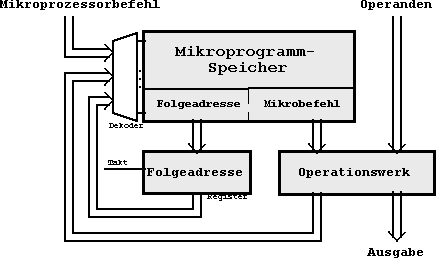
Abb. 6.14: Aufbau eines Mikroprogramm-Steuerwerkes
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |