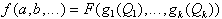 | . | (2.19) |
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |
Im letzten Kapitel wurden Funktionsbündel
eingeführt, um durch Zusammenfassung identischer Funktionen
Schaltungen zu vereinfachen.
In ähnlicher Form kann durch
Zerlegung einer Funktion in Teilfunktionen eine Schaltungsoptimierung
durchgeführt werden. Dies gilt insbesondere für umfangreiche
Verknüpfungsnetze, die auf Grund ihrer Komplexität meist
sehr unübersichtlich sind. Da sie meistens auf ein spezielles
Problem zugeschnitten sind, fehlt ihnen außerdem jede universelle
Anwendungsmöglichkeit.
Diese Netze sollten in Teilnetze
geringerer Komplexität zerlegt werden, wobei die folgenden
Optimierungskriterien zu befolgen sind:
Definition:
Eine Boolesche Funktion f(a,b,...)
ist zerlegbar in k BFkten gi(Qi)
mit i = 1,...,k und Qi {a,b,...},
wenn es eine BFkt F(1,...,k) gibt, so daß gilt:
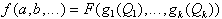| . | (2.19) |
Es entstehen auf diese Weise mehrstufige Schaltungen.
Insbesondere zwei Funktionszerlegungsformen sollen zunächst unterschieden werden:
2.10.1 Disjunkte Funktions-Zerlegung
Die BFkt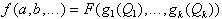 
heißt disjunkt zerlegbar, wenn für alle i,j k und i j gilt:
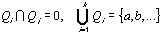 | (2.20) |
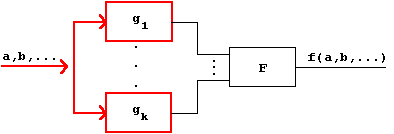
Abb. 2.40: Disjunkte Funktions-Zerlegung.
2.10.2 Iterative Funktions-Zerlegung
Eine BFkt heißt iterativ zerlegbar
in m Funktionen, wenn es eine BFkt gi(Qi) mit i = 1,...,m gibt, so daß gilt:
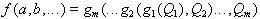 | (2.21) |
| mit: | 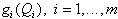 | (2.22) |
Beispiel:
Iterative Zerlegung in 2 Funktionen:
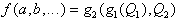 | (2.23) |
Beispiel:
Iterative Zerlegung in 3 Funktionen:
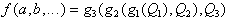 | (2.24) |
Schaltungen dieser Art haben offenbar eine Kettenstruktur (pipeline architecture):
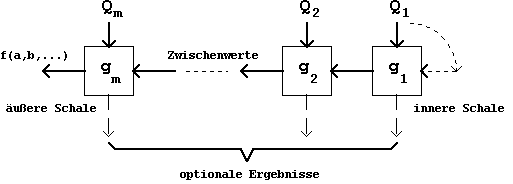
Abb. 2.41: Iterative Funktions-Zerlegung
2.10.3 Funktionszerlegungen:
Beispiele
Die Möglichkeit der Funktionszerlegung
soll an zwei charakteristischen, praktischen Beispielen aufgezeigt werden.
Beispiel 1: Paritätsprüfung
(Disjunkte Zerlegung)
Unter Paritätsprüfung versteht
man den Nachweis, daß in einer vorgegebenen Zahl von Signalen
die Anzahl der 1-Signale gerade oder ungerade ist. Man definiert
entsprechend:
Es soll die Prüfung der ungeraden
Parität in einer disjunktiven Normalform (DNF) formuliert
werden. Mit Hilfe eines KV-Diagrammes kann das Problem zunächst
anschaulich definiert werden (mit 1 markiert werden alle Felder,
für die die Anzahl der 1-Argumente ungerade ist):
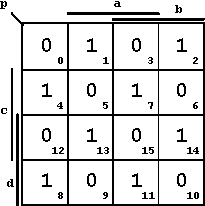
Abb. 2.42: KV-Diagramm der Booleschen Funktion zur Prüfung auf ungerade Parität.
Für die ungerade Parität
ergibt sich demnach folgende DNF-Beschreibung (disjunktive Normalform):
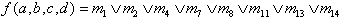
Bewertung der Funktionsimplementierung:
Nach den oben eingeführten Kriterien
kann diese Schaltung bewertet werden, indem Gatterlaufzeit und
Gattereingangszahl (pin count) bestimmt werden:
| Gatterlaufzeit: | 2 (es handelt sich um eine Normalform) |
| pin count: | c = 40 (c = 8*4 + 8: 8 Gatter mit 4 Eingängen, 1 ODER-Gatter mit 8 Eingängen) |
Die BFkt zur Bestimmung der ungeraden
Parität kann außerdem unter Benutzung der Funktion
XOR (Exklusives ODER, EXOR, mathematisches Verknüpfungssymbol: )
in verkürzter Form beschrieben werden.
Definition der XOR-Funktion:
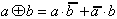 | (2.25) |
Für die vierstellige Paritätsfunktion gilt damit:
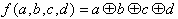 | (2.26) |
Da die Funktion XOR assoziativ ist, gilt weiterhin:
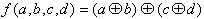 | (2.27) |
Funktionsrealisierung in einem "double rail system":
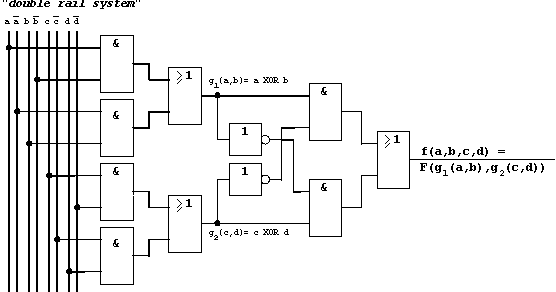
Abb. 2.43: Schaltungsrealisierung der Paritätsprüfung.
Funktionsbewertung:
| Gatterlaufzeit: | 5 (keine Normalform) |
| pin count: | c = 20 (c = 9*2 + 2*1, s.o.) |
Beispiel 2: Addier-Schaltungen (Iterative Zerlegung)
Eine Schaltung zur Addition zweier Dualzahlen (Additionswerk, Addierer) kann in einer Kettenstruktur realisiert werden.
Die folgende Funktionstabelle unterscheidet die Addierer nach
Tab. 2.9: Wertetafel eines Volladdierers; der schraffierte (rote) Bereich kennzeichnet den Halbaddierer.
Der schraffierte (rote) Teil dieser Tabelle charakterisiert den einstufigen Halbaddierer, der zwei einstellige Dualzahlen (d.h. zwei Bits) summiert, das Ergebnis s bildet und das Übertragsbit c (carry bit) bestimmt.
Der einstufige Volladdierer arbeitet
wie der Halbaddierer, berücksichtigt aber außerdem
den Übertrag aus der Addition in einer vorhergehenden Position.
In diesem Fall gibt es also zwei Übertragsbits: der Eingangsübertrag
(carry in, cIN)
und der Ausgangsübertrag (carry out, cOUT).
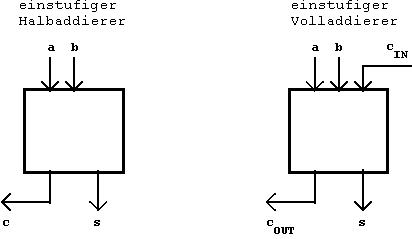
Abb. 2.44: Einstufiger Halb- und Volladdierer.
Der Volladdierer erlaubt die Realisierung mehrstufiger Addierer:
Kettenstruktur eines n-stelligen Volladdierers (ripple adder):
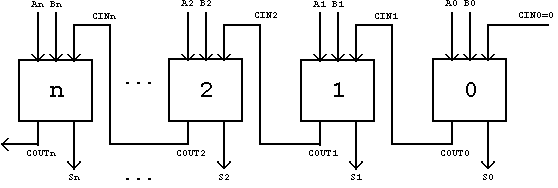
Abb. 2.45: n-stufiger Volladdierer.
Aus der o.a. Wertetabelle ergibt
sich unmittelbar für die BFkten s (Summenbit) und cOUT
(carry out):
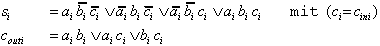 | (2.28) |
Gleichwertige Formulierungen für beide Gleichungen sind:
 | (2.29) |
Würde die Addier-Funktion nicht,
wie hier gezeigt, iterativ zerlegt werden, so sind bei einem n-stufigen
Addierer Gatter mit einer Eingangsbreite von n + 1 erforderlich.
Für n > 8 ist dies nicht mehr zweckmäßig,
so daß in diesem Fall eine mehrstufige Schaltung sogar als
notwendig angesehen werden kann.
Eine weitere wichtige Zerlegungsmethode wird als Shannon-Zerlegung bezeichnet.
Definition: Für jede BFkt f(a,b,...)
existiert eine nicht-disjunkte Zerlegung, für die gilt:
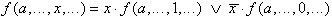 | (2.30) |
Diese Funktionszerlegungsmethode folgt unmittelbar aus der ursprünglichen Definition und Entwicklung des KV-Diagramms. Hinzunahme einer Variablen bedeutete ja die Verdoppelung der Felderzahl:
Wird f(a,b) um ein Argument c erweitert,
so kann ein Feld f(a,b) für c = 0 definiert werden
und ein zweites Feld f(a,b) für c = 1. Aus f(a,b) wird schließlich
f(a,b,c), indem die beiden Einzeldiagramme aneinandergefügt
werden.
Bei der Shannon-Zerlegung wird dieser
Prozeß also lediglich in umgekehrter Richtung durchlaufen;
es wird eine Halbierung des KV-Diagramms der BFkt f(a,...,x,...)
bezüglich der Variablen x vorgenommen.
f(a,...,1,...) beschreibt dann die Funktion im Bereich x = 1,
f(a,...,0,...) beschreibt die Funktion im Bereich x = 0.
Ist also f(a,...,1,...) = 1
oder f(a,...,0,...) = 1, dann liefert auch die Disjunktion
f(a,...,x,...) = 1. Nur wenn beide Term-Funktionen den
Wert '0' annehmen, ergibt sich auch für die Gesamtfunktion
f(a,...,x,...) = 0.
Die Shannon-Zerlegung ist auf jede
Boolesche Funktion anwendbar. Das bedeutet natürlich, daß
auch die oben gebildeten Terme f(a,...,1,...) und f(a,...,0,...)
ihrerseits mit der gleichen Methodik zerlegt werden können.
Für eine zweielementige BFkt
führt dies zur folgenden vollständigen Shannon-Zerlegung:
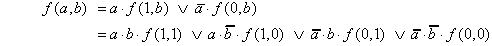 | (2.31) |
Entsprechend kann die Zerlegung einer
dreielementigen BFkt vorgenommen werden:
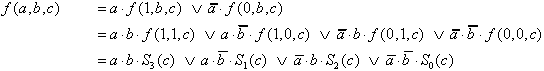 | (2.32) |
Die Numerierung der hier eingeführten
(nicht weiter zerlegten) Funktionsterme Si
folgt in gewohnter Form den Wertigkeiten der 2-Tupel (a,b).
Beispiel:
Zerlegung einer durch ein KV-Diagramm
vorgegebenen Booleschen Funktion f(a,b,c,d) bzgl. der Argumente
a und b:
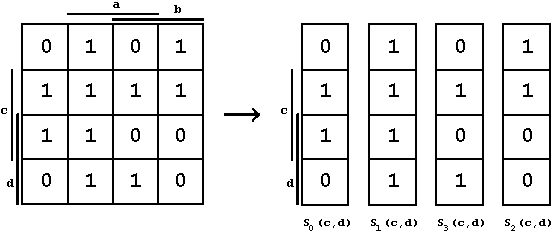
Abb. 2.46: Funktionszrelegung nach a und b.
Die anschaulich am KV-Diagramm gezeigte Funktionszerlegung kann zu einer praktischen Schaltungsimplementierung führen, falls die entstandenen Terme Si(c,d) z.B. durch einen hypothetischen "Schalter" in Abhängigkeit von (a,b) auf die Ausgangsleitung Y = f(a,b,c,d) geschaltet werden können:
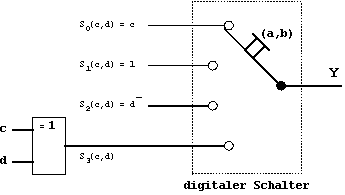
Abb. 2.47: Anwendung eines Schalters zur Funktionszerlegung.
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |