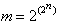 (1.3)
(1.3)
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |
Wie oben gezeigt wurde, können Boolesche Funktionen (auch Schaltfunktionen genannt) in vielfältiger Form dargestellt werden.
Im Prinzip ist eine Boolesche Funktion eine Zuordnungsvorschrift,
die formal über einen mathematischen Ausdruck definiert werden
kann.
Neben dieser mathematischen Beschreibungsform existiert eine
weitere formale Darstellungsmethode über Wahrheitstafeln,
d.h. über eine tabellarisch geordnete Wiedergabe des funktionalen
Zusammenhanges.
Betrachten wir eine Boolesche Funktion f, die n Argumente
xi hat, dann erhalten wir folgende generische Wahrheitstafel (Wertetabelle):
wobei gilt: fi {0,1}
Wie ersichtlich, wird in dieser Tabelle in 2
Da in jeder Zeile entweder der Funktionswert 0 oder 1 angenommen
wird, gibt es
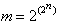 (1.3)
(1.3)
nichtäquivalente Funktionen f(x1,x2,...,xn).
Im einfachsten Fall hängt die Boolesche Funktion nur
von einer einzigen Variablen ab (s.o. unäre Funktionen),
so daß
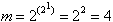
verschiedene Funktionen existieren.
Bei zwei Variablen (binäre Boolesche Funktionen) existieren entsprechend
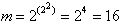
unterschiedliche Funktionen.
Es zeigt sich also, daß die Anzahl der möglichen Booleschen Funktionen mit steigender Variablenzahl n sehr stark zunimmt.
In der folgenden Behandlung wird allerdings erkennbar werden,
daß nur einige wenige dieser Funktionen nicht-triviale Eigenschaften
besitzen und daher für die praktische Anwendung von Bedeutung
sind.
Von den vier möglichen Booleschen Funktionen einer Variablen
(n=1) ist bereits die wichtigste eingeführt worden, die "Negation"
(Invers-Funktion, s.o.).
Die folgende Tabelle gibt einen Überblick über alle
Funktionen mit Hilfe der entsprechenden Wahrheitstafeln, funktionalen
Ausdrücke und Venn-Diagramme. Wo immer sinnvoll, ist außerdem
das in der Digitaltechnik verwendete Schaltsymbol (nach DIN/IEC)
angegeben.
| Name | |||||
| Wahrheitstafel | |||||
| Ausdruck | 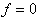 | 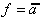 | 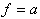 | 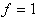 |
|
| Venn-Diagramm |  |  |  |  |
|
| Schaltsymbol
(DIN/IEC) | 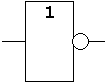 |
In der folgenden Zusammenstellung der binären Booleschen
Funktionen werden für die wichtigsten Funktionen die gebräuchlichsten
Namen sowie die DIN-Schaltsymbole angegeben.
| Name | 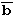 | |||||
| Wahrheitstafel | ||||||
| Ausdruck |
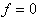 | 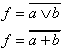 | 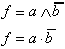 |
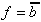 | ||
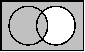
| Venn-Diagramm | 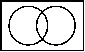 | 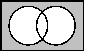 | 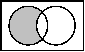 | 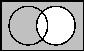 | ||
| Schaltsymbol (DIN/IEC) | 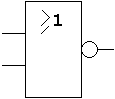 |
| Name | 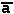 | |||||
| Wahrheitstafel | ||||||
| Ausdruck | 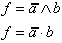 | 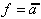 | 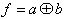 | 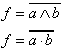 |
||
| Venn-Diagramm | 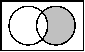 | 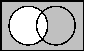 | 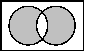 |  |
||
| Schaltsymbol (DIN/IEC) | 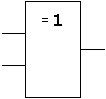 | 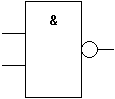 |
| Name |
| |||||
| Wahrheitstafel | ||||||
| Ausdruck | 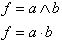 | 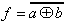 |
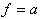 | 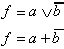 | ||
| Venn-Diagramm | 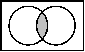 | 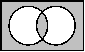 |
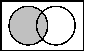 |  | ||
| Schaltsymbol (DIN/IEC) | 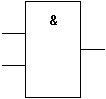 | 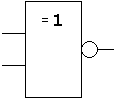 |
| Name |
|
| ||||
| Wahrheitstafel | ||||||
| Ausdruck | 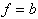 | 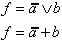 | 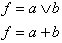 | 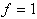 | ||
| Venn-Diagramm | 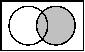 | 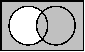 | 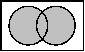 | 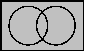 | ||
| Schaltsymbol (DIN/IEC) | 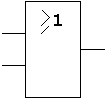 |
Wie gezeigt wurde, wächst die Anzahl der definierbaren
Booleschen Funktionen mit Erhöhung der Anzahl der Argumente
sehr stark an. Für n = 3 ergeben sich bereits m = 256 mögliche
Funktionen, die größtenteils bedeutungslos sind.
Die Digitaltechnik beschränkt sich daher auch bei n >= 3
auf die von n = 2 her bekannten wichtigen Funktionen
und den zugehörigen Schaltzeichen bei entsprechender Erhöhung
der Anzahl der Eingangs-Variablen (s.u. UND- bzw. ODER-Funktion).
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |