| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |
Werden n Mengen durch eine Funktion (Operation) miteinander
verknüpft, so wird diese Funktion auf alle möglichen
n-Tupel der Einzelelemente, den Funktionsargumenten, angewendet.
Erläuterung der Schreibweise:
Eine Boolesche Funktion f verknüpfe zwei Operanden a und b:
Dann wird die BFkt f(a,b) angewendet auf die Elementpaare (2-Tupel)
Das Ergebnis dieser Operation f(a,b) kann wiederum durch Mengen
beschrieben werden, die Ergebnismengen. Da als Ergebniswerte der
Booleschen Funktion f nur die Werte 0 und 1 möglich sind,
kann das Ergebnis mit Hilfe der 0-Menge und der 1-Menge gekennzeichnet
werden:
Auch für eine n-stellige Boolesche Funktion kann das
Ergebnis natürlich in entsprechender Form beschrieben werden.
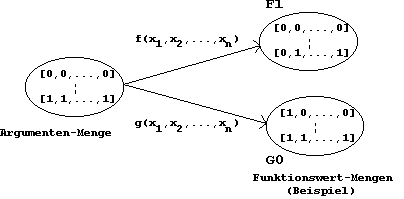
Die BFkt f(a0,a1,...,an) ordnet jedem ihrer Argumente (n-Tupel)
einen Funktionswert "0" bzw. "1" zu, sie "sortiert"
die n-Tupel in die Mengen F0 bzw. F1:
Die Boolesche Funktion bildet die Argumenten-Menge auf die Funktionswert-Mengen ab.
Diese Verhältnisse können in grafischer Form veranschaulicht werden:

Beispiel: Die binäre Boolesche Funktion: UND
Definition:
Die BFkt UND liefert dann und nur dann den Funktionwert "1",
wenn alle Funktionsargumente den Wert "1" haben.
Damit ergibt sich unmittelbar die Beschreibung der Lösungsmengen:
was wiederum grafisch dargestellt werden kann:
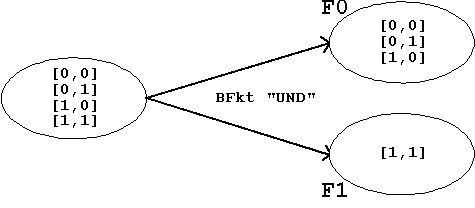
Abb. 1.4: Die Boolesche Funktion "UND"
Es bestehen andere Möglichkeiten eine Boolesche Funktion zu charakterisieren.
Häufig Verwendung findet die Beschreibung durch Tabellen,
die in diesem Fall dann als "Funktionstabellen" bezeichnet
werden. Andere synonyme Namen sind "Wertetabelle", "Wahrheitstafel"
oder ähnliche Formulierungen.
Beispiel: Wahrheitstafel der Funktion "UND":
Eine weitere Beschreibungsform definiert die Boolesche Funktion
mit Hilfe eines mathematischen Verknüpfungssymbols (ähnlich
wie dies z.B. bei der Beschreibung der Grundrechenarten durch
die Symbole +, -, ... geschieht). In einigen Fällen, wie
auch hier bei der Funktion "UND", stehen mehrere, in
ihrer Bedeutung äquivalente Symbole zur Verfügung.
Beispiel: Verknüpfungssymbol
der Funktion "UND":
Begriffe wie "digitale Schaltung", "Schaltungstechnik"
usw. deuten an, daß (elektromechanische) Schalter (Relais)
einmal von entscheidender Wichtigkeit in der Elektronik waren.
Obwohl ihre Bedeutung heute nur noch untergeordnet ist, können
Schalter weiterhin herangezogen werden, um das logische Verhalten
Boolescher Funktionen zu verdeutlichen.
Beispiel: Schalterimplementierung der Funktion "UND" (s.o.):
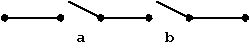
Abb. 1.5: "UND"-Funktion.
Dieses Kontaktschema zeigt, daß eine Reihenschaltung
zweier Schalter a und b nur dann zur Aktivierung z.B. eines nachgeschalteten
Verbrauchers führt, wenn sowohl a als auch b geschlossen
sind.
Wird dieser geschlossene Zustand mit "1" interpretiert,
so entspricht dies genau dem Verhalten der oben über eine
Wahrheitstafel definierten BFkt "UND".
Eine mengenorientierte Darstellung der Booleschen Funktionen
kann in einer weiteren grafischen Form vorgenommen werden, die
als Venn-Diagramm bekannt ist.
In diesem Venn-Diagramm werden die Argumenten-Mengen und die
Ergebnis-Menge derart zusammengefaßt, daß eine einfache
Interpretation möglich wird.
Die beiden Mengen werden durch unterschiedliche Merkmale charakterisiert:
Am Beispiel einer einfachen unären Funktion kann dieser
Sachverhalt genauer aufgezeigt werden:
Beispiel: Die unäre
Funktion "NOT" (NEGATION, INVERS-Funktion):
Diese Funktion wirkt nur auf einen einzigen Parameter ein
(unär). Sie invertiert den logischen Wert des Arguments,
d.h.
Sei U eine Bezugsmenge (Universalmenge), in der auch die Menge
A enthalten sei. Es kann dann die Komplementmenge (oder Ergänzungsmenge)
zu A definiert werden, die alle Elemente umfaßt, die zwar
in U aber nicht in A enthalten sind.
CU(A) ist die Komplementmenge von A bezüglich U.
Das entsprechende Venn-Diagramm sieht also folgendermaßen aus:
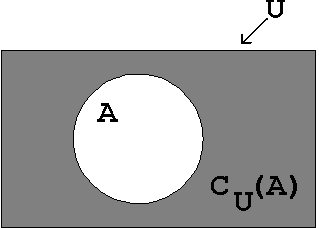
Abb. 1.6: Venn-Diagramm der INVERS-Funktion
Um auch umfangreichere digitale Schaltungen zu behandeln, können natürlich die oben eingeführten Darstellungsmethoden herangezogen werden, z.B. die Mengendarstellung, die funktionale Beschreibung, etc..
Bei der Entwicklung komplexer Schaltungen führt dies aber sehr schnell zur Unübersichtlichkeit. Durchgesetzt hat sich daher eine Methode, die grafische Symbole, sogenannte Schaltzeichen (Schaltsymbole) heranzieht, um die einzelnen Funktionen (Verknüpfungen) zu charakterisieren.
Diese Schaltzeichen sind auf internationaler Ebene genormt
und erlauben daher eine eindeutige und vollständige (logische)
Beschreibung digitaler Schaltungen.
Leider kann nicht von einer einzigen Normierung gesprochen
werden. Auf Grund der historischen Entwicklung gibt es unterschiedliche
Schaltzeichen-Normen, die zum Teil auch heute noch unabhängig
voneinander zur Anwendung kommen:
Normen a und b kommen in den entsprechenden Ländern zur
Anwendung, während es sich bei Norm c um eine alte DIN-Version
handelt, die heute auf alle Fälle vermieden merden sollte.
Beispiel: Schaltsymbole für die Funktion "Negation"
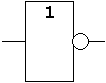 |
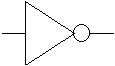 | 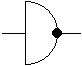 |
Hinweis:
Ähnliche Schaltzeichen existieren für Boolesche Funktionen mehrerer Variablen (s.u.).
Die oben eingeführten Venn-Diagramme können auch
dann zur grafischen Veranschaulichung herangezogen werden, wenn
neue, komplexere Boolesche Funktionen durch Verknüpfung mehrerer
Einzelfunktionen erzeugt werden.
Seien f1(a,b) und f2(a,c) zwei binäre BFkten, deren Argumente
a,b und c extern bewertet werden. Die Ergebnisse von f1 und f2
sollen dann als Eingangsargumente einer dritten binären Funktion
f3(g,h) dienen. Das Funktionsergebnis f3 hängt also von a,b
und c ab.
Der Sachverhalt kann wiederum grafisch dargestellt werden,
wenn die Einzelfunktionen z.B. durch Kästchen symbolisiert
werden:
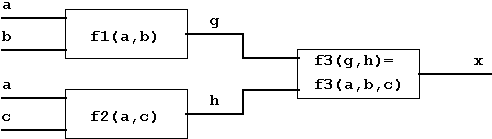
Abb. 1.8:
Verknüpfung zweier Boolescher Funktionen.
In ähnlicher Form werden in der Digitaltechnik (Schaltungs-technik) alle logischen Operationen symbolisch definiert.
Die gleiche Funktionsverknüpfung kann auch wieder durch
Angabe der Argumenten- und Funktionswertmengen verdeutlicht werden:
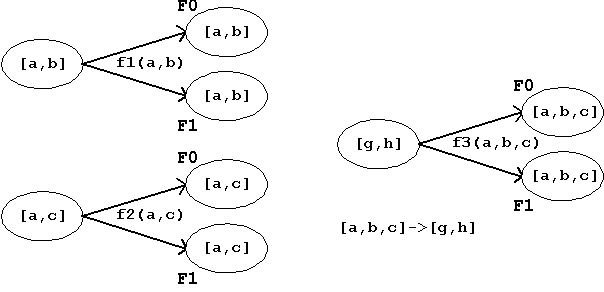
Abb. 1.9:
Mengendarstellung einer Funktionsverknüpfung.
Sollen zur Darstellung wiederum Venn-Diagramme herangezogen
werden, so bietet es sich in diesem komplexeren Fall an, die einzelen
Argumentenelemente (Element-Tupel) anschaulicher zu repräsentieren
(z.B. wiederum durch farb- oder schattierungs-markierte Punkte
bzw. Kreise). Im Falle obiger Beispielfunktion könnte dies
dann folgendermaßen aussehen:
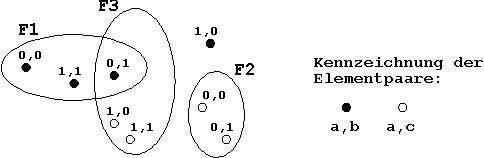
Abb. 1.10:
Venn-Diagramm-Darstellung einer Funktionsverknüpfung.
Für die 1-Mengen F1, F2 und F3 gilt dann:
Also:
Die hier gezeigte Funktionsdefinition ist eindeutig für
f1 und f2, nicht aber für f3, was z.B. am Funktionswert f3(1,0,0)
verifiziert werden kann.
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |