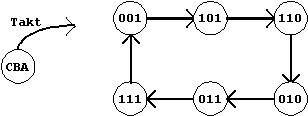
Abb. 7.5: Zustandsdiagramm des Modulo-6-Zählers.
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |
In einer ersten praktischen Anwendung
soll ein Modulo-6-Zähler entworfen werden. An diesem Beispiel
können die allgemein gültigen Entwurfsphasen demonstriert
werden.
Dieser Zähler soll in einer
Sequenz zählen, die bereits in Form eines Zustandsdiagrammes
definiert wurde:

Abb. 7.5: Zustandsdiagramm des Modulo-6-Zählers.
Um die Zählgeschwindigkeit zu optimieren, soll bei diesem Entwurf auf ein Ausgabe-Verknüpfungsnetz verzichtet werden; die auszugebene Zählsequenz wird also der Zustandskodierung entsprechen.
Hinweis:
Bei obiger Zustandskodierung wurde bewußt auf den Code '000' verzichtet. Dieser Zustand ist zwar sehr leicht durch ein Rücksetzen der Flipflops ("reset") realisierbar, er läuft allerdings meistens asynchron ab und kann daher über den Zählerausgang zu Systemstörungen führen.
Zähler werden in einer Form
entwickelt, die als "top-down"-Methode bezeichnet
werden kann: man beginnt mit der allgemeinen Beschreibung und
endet mit der schaltungstechnischen Realisierung.
Die folgenden beiden Entwurfsschritte
können dementsprechend unterschieden werden:
1. Schritt: Bestimmung der Anzahl der benötigten Flipflops und der Zustandskodierung.
Bei einem vorgegebenen Zählumfang
"modulo-m" sind bei einer Binärkodierung mindestens
n Flipflops notwendig, wobei gilt:
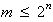
Außer dieser "effektiven"
Binärkodierung der Zustände gibt es andere Kodierungsmethoden,
bei denen aber fast immer eine größere Anzahl von Flipflops
notwendig wird (z.B. "1-aus-n"-Code oder einschrittige
Codes wie der Gray-Code oder der Johnson-Zählcode, siehe
Kap. 2 und 8). Im "1-aus-n"-Code z.B.
ist jedem Zustand ein Bit zugeordnet, so daß in diesem Fall
insgesamt also genau 2n
Flipflops erforderlich sind.
Im Entwurfsbeispiel (Modulo-6-Zähler)
sind nur drei Flipflops einzusetzen. Da die Gesamtzahl der möglichen
Zustandskodierungen damit 2n = 8
beträgt, ergeben sich zwei ungenutzte Zustände (freie
"Triaden" oder "Pseudotriaden"): '000' und
'100'.
2. Schritt:
Auswahl des Flipfloptyps und Entwurf des Verknüpfungsnetzes.
Als Flipfloparten werden meistens
D-Flipflops oder (wegen des größeren Funktionsumfangs)
JK-Flipflops eingesetzt. Die Taktung ist einflankig (vorder- bzw.
rückflankengesteuert). In einem synchronen Zähler müssen
für jeden Zustandsübergang alle Flipflop-Eingänge
definiert angesteuert werden.
Ausgehend von dem Zustandsdiagramm wird die Zählsequenz zunächst noch FF-unabhängig in einem Übergangsdiagramm dargestellt (u.U. unter Benutzung einer optionalen Übergangstabelle).
Danach erfolgt eine FF-spezifische
Darstellung in KV-Diagrammen, die in diesem Zusammenhang als Anwendungs-Diagramme
bezeichnet werden.
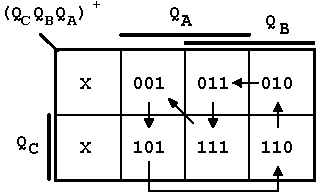
Abb. 7.6: Übergangsdiagramm des Modulo-6-Zählers.
In jedem Feld dieses Übergangsdiagramms
wird der Zählerstand in der vorgegebenen Kodierung (hier
QCQBQA)
eingetragen. Der Eintrag entspricht also den Feldkoordinaten.
Durch Pfeile wird dann die Zählsequenz angegeben, so daß bereits in dieser Anordnung das Wechseln der einzelen Zustandsbits sichtbar wird.
Zum Auffinden der Lösung mit D-Flipflops werden für die Eingänge Di die notwendigen Ansteuerungen in individuelle KV-Diagramme eingetragen. Diese Gesamtheit der Diagramme wird als Anwendungsdiagramme bezeichnet.
Bei D-Flipflops ist dies besonders einfach, da ja immer gilt:
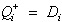 | . | (7.1) |
Für jedes Zustandsbit wird ein
Anwendungsdiagramm aufgestellt, in dem jedes Feld den gemäß
Übergangsdiagramm mit dem nächsten Taktsignal folgenden
Wert des Zustandsbits enthält:

Abb. 7.7: Anwendungsdiagramme für den Modulo-6-Zähler.
Aus diesen Anwendungsdiagrammen lassen
sich dann (nach Verbundbildung) die Funktionsgleichungen für
die Eingänge Di ableiten:
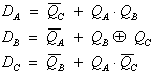 | (7.2) |
Für einen Zählerentwurf mit JK-Flipflops ist es günstiger, das Übergangsdiagramm bereits JK-spezifisch aufzustellen.
Es ist daher sinnvoll, im KV-Diagramm
direkt die Wertewechsel der Zustandsbits anzugeben. Aus dieser
Angabe Q 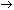 Q+
kann dann sofort die erforderliche Ansteuerung der Flipflops ermittelt
werden.
Q+
kann dann sofort die erforderliche Ansteuerung der Flipflops ermittelt
werden.
Aus dem Übergangsdiagramm für eine Modulo-6-Zähler-Realisierung mit D-Flipflops (s.o.) können die folgenden Übergangsdiagramme für die zum gleichwertigen Aufbau erforderlichen JK-Flipflops aufgestellt werden:
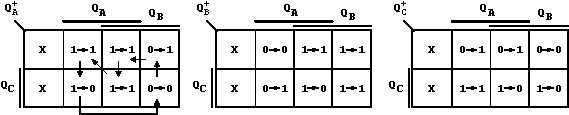
Abb. 7.8: Übergangssdiagramme für den Modulo-6-Zähler.
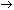 Q+ Q+ | |||
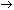 0 0 | |||
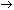 1 1 | |||
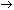 0 0 | |||
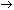 1 1 |
Abb. 7.9: Übergangstabelle für das JK-Flipflop.
Unter Beachtung der bereits bekannten
Übergangstabelle des JK-Flipflops können aus diesen
Übergangsdiagrammen dann schließlich die entsprechenden
Anwendungsdiagramme hergeleitet werden:
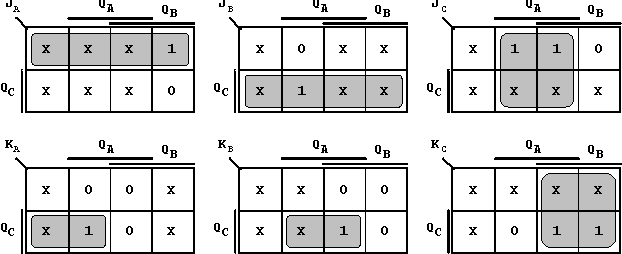
Abb. 7.10: Anwendungsdiagramme für den Modulo-6-Zähler in JK-Realisierung (mit zur Vereinfachung gebildeten Feldverbunden).
Aus den KV-Diagrammen können jetzt die Funktionsgleichungen für die Ji und Ki bestimmt werden. Für Flipflop A ergibt sich beispielsweise:
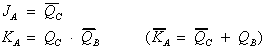 | (7.3) |
Die J-K-Ansteuerung kann auch über
die charakteristische Gleichung des JK-Flipflops entwickelt werden:
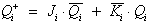 | , |
bzw. für QA:
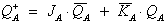 | . |
Aus Abb. 7.8 folgt:
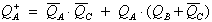 | (7.5) |
Der Vergleich von Gl. 7.4 mit
Gl. 7.5 ergibt die in Gl. 7.3 wiedergebene Lösung.
Entsprechend können die Lösungen für QB
und QC ermittelt werden.
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |