Abb. 1.1: Verwendung von Zählbrettern in der Antike
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |
Die Aufgabe der Digitaltechnik ist
die Darstellung und Verarbeitung von Informationen (Informationsverarbeitung).
Um eine einfache physikalische Realisierung dieser Informationsverarbeitung
zu gewährleisten, bedient sich die Digitaltechnik eines eingeschränkten
Zeichensatzes, der auf eine Minimalform reduziert wurde:
Es werden zur Informationsdarstellung
nur zwei Wertigkeiten bzw. Zeichen verwendet. In Abhängigkeit
von dem betrachteten System können diese beiden zur Beschreibung
notwendigen Zeichen in unterschiedlicher Form definiert werden,
z.B.:
| Digitaltechnik | "0" und "1" |
| Physik | "low" und "high" |
| Aussagenlogik | "wahr" und "falsch" bzw. "true" und "false" |
Die Eigenschaft, jeweils einen von
zwei Werten oder Zuständen annehmen zu können, wird
als "binär" (lat.: aus zwei Einheiten bestehend;
engl. binary) bezeichnet.
Das Wort "digital" soll
im Gegensatz zum Wort "analog" die Abzählbarkeit
einer Informationsmenge zum Ausdruck bringen. Während ein
analoges System eine unendlich große Abstufung von Wertigkeiten
erlaubt, gibt es im digitalen System nur genau differenzierbare,
"diskrete" Werte, die in einfachster Form abgezählt
werden können, z.b. mit den Fingern. Auch die alten Römer
konnten dies schon. Ihre Finger (lat. digitus) sind "schuld"
daran, daß wir heute von "Digitaltechnik"
sprechen.
Dieses an den "Finger abzählen" ist natürlich auch der Grund dafür, daß wir im täglichen Leben das sogenannte "Dezimalsystem" (Zehnersystem) verwenden. Da in der Technik kein Grund zum "Zehnfingersystem" besteht, wird dort wegen der leichteren technischen Realisierung das oben definierte "Zweifingersystem" eingesetzt.
Wegen seiner Beschränkung auf
nur zwei Zeichen, wird dieses Darstellungssystem als
"dual"
bezeichnet (duales Zahlensystem).
Viele Begriffe der Digitaltechnik
werden mit Bezeichungen und Abkürzungen belegt, die unmittelbar
Bezug nehmen auf den lateinischen bzw. den englischen Ursprung.
Beispiel:
Die kleinste binäre Nachrichtenmenge,
das Binärzeichen, wird als "Bit" bezeichnet, was
der englischen Bezeichnung "binary
digit" entstammt.
Ein Bit beschreibt also den logischen
Zustand eines zweiwertigen Systems. Die Tatsache, daß es
sich um ein minimales System handelt, kommt in der ursprünglich
durch Claude Shannon eingeführten Bezeichnung zum Ausdruck:
Die Begriffe, die in der Digitaltechnik
bzw. der Informationsverarbeitung zur Anwendung kommen, sind weitestgehend
genormt. Genauere Informationen können in den entsprechnenden
DIN- bzw- IEC-Publikationen gefunden werden.

Abb. 1.1: Verwendung von Zählbrettern in der Antike
Natürlich bietet die maschinenorientierte
duale Zeichendarstellung im alltäglichen Leben keinen Vorteil.
Im Gegenteil, die technisch leicht implementierbare "0/1"-Darstellung
ist für uns schwer lesbar und gibt daher leicht zu fehlerhafter
Interpretation Anlaß.
Beispiel:
Die duale Zeichenkette
scheint einer willkürlichen
Informationsfolge zu entsprechen, obwohl es sich nur um die populärste
Form der binären Darstellung der ersten drei Buchstaben unseres
Alphabets handelt:
Die hier gewählte Binärdarstellung
entspricht der Definition des sogenannten ASCII-Zeichensatzes,
der im Kapitel "Zahlen und Codes" ausführlicher
behandelt wird.
Um uns den Umgang mit solchen Informationen
zu vereinfachen, könnte natürlich weiterhin das gewohnte
Dezimalsystem zum Einsatz kommen, wodurch allerdings die Nähe
zur binären Darstellung verlorengänge.
Die Einführung zweier neuer
Systeme dient deshalb der verbesserten Lesbarkeit bei Aufrechterhaltung
der Beziehung zur dualen Informationsdarstellung. Diese neuen
Systeme werden bezeichnet als:
| Oktalsystem |
| Hexadezimalsystem. |
Zeichen in diesen neuen Systemen können unmittelbar über die duale Darstellung definiert werden. Es reicht eine Gruppierung entsprechender Bits in größere Einheiten.
Im obigen Beispiel könnte die Beziehung zum ASCII-System durch eine Unterteilung in Gruppen von jeweils acht Bits verdeutlicht werden:
| dual: | 01000001 | 01000010 | 01000011 |
| ASCII: | A | B | C |
In ähnlicher Weise werden beim
Übergang zum Oktalsystem Dreiergruppen, beim Übergang
zum Hexadezimalsystem Vierergruppen gebildet:
Zum besseren Verständnis werden
die Bit-Gruppen dann wiederum durch Wertigkeiten ersetzt, die
unserem Dezimalsystem entsprechen. Im Falle des Oktalsystems ist
dies ohne Komplikation möglich, da die größtmögliche
Bitrepresentation im Oktalsystem ("111") eine äquivalente
Dezimalrepresentation besitzt ("7"). Im Falle des Hexadezimalsystems
besteht das Problem einer Dezimalrepresentation für Zahlen,
deren Wertigkeit die Zahl 9 übersteigt, nämlich:
Um auch diese Zahlen mit einem einzigen Zeichen ausdrücken zu können, werden die ersten sechs Buchstaben unseres Alphabets herangezogen, so daß zur Definition einer beliebigen Hexadezimalzahl schließlich die folgenden Symbole zur Verfügung stehen:
Mit diesen Definitionen ist eine tabellarische Gegenüberstellung der Zahlensysteme möglich:
Tab. 1.2: Zahlensysteme.
Das oben diskutierte Beispiel ("ABC")
kann damit im Oktal- und Hexadezimalsystem angegeben werden:
| oktal | 010 | 000 | 010 | 100 | 001 | 001 | 000 | 011 |
| 2 | 0 | 2 | 4 | 1 | 1 | 0 | 3 |
| hexadezimal | 0100 | 0001 | 0100 | 0010 | 0100 | 0011 |
| 4 | 1 | 4 | 2 | 4 | 3 |
Auf dem Gebiet der Informationsverarbeitung
haben sich weitere Begriffsbildungen durchgesetzt, mit dem Ziel,
oft benutzten Bit-Gruppierungen Namen zu geben. Besonders wichtig
auch in der Digitaltechnik sind folgende Anordnungen bzw. Definitionen:
| 1 Byte | = | 1 Gruppe von 8 Bits |
| 1 Nibble | = | 1 Gruppe von 4 Bits. |
Damit ergibt sich folglich:
| 1 Byte | = | 2 Nibble. |
Weitere Gruppierungen (word, double word, etc.) sind in der Informatik üblich, sollen hier aber zunächst übergangen werden.
Die Benutzung der oben definierten
Zahlensysteme ist in der Digitaltechnik außerordentlich
wichtig, dies schließt natürlich auch die "Übersetzung"
zwischen den Systemen ein. Im Kapitel "Zahlen und Codes"
wird deshalb in detaillierter Form auf dieses Thema eingegangen.
Schon an dieser Stelle kann allerdings
der Umgang mit den unterschiedlichen Zahlensystemen dadurch vereinfacht
werden, daß ihre Behandlung buchstäblich auf eine konkrete
Basis gestellt wird:
Alle vier eingeführten Zahlensysteme gehören zu den sogenannten polyadischen Zahlensystemen. Ein polyadisches Zahlensystem mit der Basis B, auch B-adisches Zahlensystem genannt, ist ein Zahlensystem, in dem eine Zahl nach Potenzen von B zerlegt wird.
Eine natürliche Zahl n kann
also durch folgende Summe von Potenzen dargestellt werden:
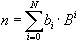 | , | (1.1) |
wobei gilt:
| B ist die Basis des Zahlensystems: | 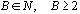
|
| und: | |
| bi sind Zahlenkoeffizienten: | 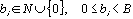 . . |
Mit dieser Definition erhält man die obigen Zahlensysteme durch entsprechende Wahl der Basis B:
| Basis | Zahlensystem |
|---|---|
| 2 | Dualsystem |
| 8 | Oktalsystem |
| 10 | Dezimalsystem |
| 16 | Hexadezimalsystem |
In der gängigen Schreibweise
werden Zahlen definiert durch Angabe der oben eingeführten
Koeffizienten bi.
Da in den unterschiedlichen Zahlensystemen
die gleichen Symbole eingesetzt werden, ist es oftmals nicht möglich
zu entscheiden, aus welchem System eine vorgegebene Zahl stammt.
Liegt so ein Fall vor, muß die gewählte Basis explizit
angegeben werden. Normalerweise geschieht dies in Form eines Indizes.
Das führt zu folgender Konvention
für eine systemunabhängige Ziffernschreibweise:
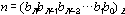 | . | (1.2) |
Es gilt hierbei:
Damit ergibt sich für das Beispiel in entgültiger Form:
| (010000010100001001000011)2 | |
| = | (10000010100001001000011)2 |
| = | (20241103)8 |
| = | (414243)16 |
Hinweis:
Die vorher eingeführten unterschiedlichen
Methoden, die zur Beschreibung der zwei möglichen Zustände
eines dualen Systemes existieren (0/1, true/false,
high/low), deuten bereits an, daß die "Elementarsymbole
0 und 1" nicht immer eine rein numerische Bedeutung haben.
In der Digitaltechnik wird häufig
eine direkte Beziehung zwischen diesen Symbolen und der physikalischen/elektronischen
Realität hergestellt. Dies führt zu Assoziationen wie:
| "1" bedeutet | "aktiv" | , |
| "0" bedeutet | "passiv" | . |
| Inhalt | Vorheriges Kapitel | Nächstes Kapitel |