Figure. 1.1: Using counting tables in the ancient world
| Contents | Previous Chapter | Next Chapter |
The objective of digital design is the representation and processing of information (information processing). To ensure a simple physical realization of information processing, digital design uses a limited character set, which was reduced to a minimal form:
To present information only two values or characters are used. Depending on the system in use these two values (states) can be defined in different ways, including:
| Digital Design | "0" and "1" |
| Physics | "low" and "high" |
| Propositional Logic | "true" and "false" |
The property of being able to take one of two values or states, respectively, is called "binary" (from Latin "consisting of two units")
Contrary to the word "digital" the word "analog" indicates a countable amount of information. While an analog system allows an infinite gradation of information (values), there are only precisely differentiable "discrete" values available in the digital system that can be counted in the simplest form, e.g. with our fingers. The ancient Romans could already do this. Their fingers (Latin digitus) are the reason that we speak today of "digital design".
This "counting with fingers" of course is also the reason that we use the so-called "decimal number system" in daily life. In technical applications no reason exists for using the decimal system, therefore the more easily applicable "two-finger system" is used.
Because of its limitation to only two values, this system is called "binary" (or "dual") numbering system.
In digital design many terms and abbreviations refer directly to the Latin and the English origin.
Example:
The smallest binary information unit is called a "bit" which comes from the English term "binary digit".
A bit therefore describes the logical state of a two-valued system (logic). The fact that it is a minimal system, is shown in the original description introduced by Claude Shannon:
The terms used in digital design and technology and in information processing are largely standardized. More detailed information can be found in the relevant publications (IEC, IEEE, DIN, EN, etc.).

Figure. 1.1: Using counting tables in the ancient world
Of course, the low-level dual character representation does not provide any advantage in everyday life. On the contrary, the technically easy to implement "0/1" representation is difficult to read for us and can therefore easy lead to faulty interpretations.
Example:
The sequence of bits
Therefore, two new systems are introduced for an improved readability while maintaining the relationship to the binary information system. These new systems will be referred to as:
| Octal numbering system |
| Hexadecimal numbering system. |
Characters in these new systems can be defined directly using the binary representation. It is sufficient to group corresponding bits into larger units.
In the above example, the relationship to the ASCII system can be illustrated by a division into groups of eight bits:
| binary: | 01000001 | 01000010 | 01000011 |
| ASCII: | A | B | C |
Similarly, groups of three bits are formed when transforming the information into the octal system, and groups of four bits in case of the transition to hexadecimal:
for a better understanding the bit groups are then in turn replaced by weights that correspond to our decimal system. In the case of the octal system this is possible without complication, since the maximum bit representation in octal ("111") has an equivalent decimal representation ("7"). In the case of the hexadecimal system a problem exists for the decimal representation for numbers whose values exceed the number 9, namely:
In order to express these numbers with a single character, the first six letters of our alphabet are used, so that the definition of any hexadecimal finally uses the following symbols:
With these definitions, a tabular comparison of the number systems is possible:
Table. 1.2: Numbering Systems.
The example discussed above ("ABC") can now be specified in octal and hexadecimal:
| octal | 010 | 000 | 010 | 100 | 001 | 001 | 000 | 011 |
| 2 | 0 | 2 | 4 | 1 | 1 | 0 | 3 |
| hexadecimal | 0100 | 0001 | 0100 | 0010 | 0100 | 0011 |
| 4 | 1 | 4 | 2 | 4 | 3 |
In the field of information processing, further conceptual structures have prevailed to give names to often used bit groupings. Particularly important in digital design are the following arrangements and definitions:
| 1 Byte | = | 1 group of 8 Bits |
| 1 Nibble | = | 1 group of 4 Bits. |
Consequently, this results in:
| 1 Byte | = | 2 Nibbles. |
Other groupings (word, double word, etc.) are common in computer science, but will not be treated at this point.
The use of the above defined number systems is extremely important in digital technology, including of course the "translation" between the systems. In the chapter "Numbers and Codes" this topic will therefore be discussed in detailed form.
Already at this point, however, dealing with the different number systems can be simplified by the fact that their treatment can literally be put on a concrete base:
All four numbering systems introduced belong to the so-called polyadic systems. A polyadic number system with base B, also called B-adic number system, is a number system in which a number is expressed as powers of B.
A natural number n can thus be represented by the following sum of powers:
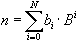 | , | (1.1) |
wherein:
| B is the base of the number system: | 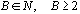
|
| and: | |
| bi are numerical coefficients: | 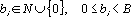 . . |
With this definition we obtain the above number systems by appropriately selecting the base B:
| Base | Numbering System |
|---|---|
| 2 | Binary System |
| 8 | Octal System |
| 10 | Decimal System |
| 16 | Hexadecimal System |
In the standard notation numbers are defined by means of the coefficients bi introduced above.
Since the same symbols are used in different number systems, it is often not possible to decide from which system a predetermined number is derived fro. If we have such a case, the selected base must be explicitly specified. Usually this takes the form of an index.
This leads to the following convention for a system-independent numeric notation:
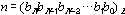 | . | (1.2) |
The following rule applies in this case:
This results in the final form for the example.
| (010000010100001001000011)2 | |
| = | (10000010100001001000011)2 |
| = | (20241103)8 |
| = | (414243)16 |
Please observe:
The previously introduced different methods to describe the two possible states of a binary system (0/1, true / false, high / low), already indicate that the basic symbols "0 and 1" do not always have a purely numerical meaning.
In digital design a direct relationship between these symbols and the physical / electronic reality is often produced. This leads to such associations as:
| "1" means | "active" | , |
| "0" means | "passive" | . |
| Contents | Previous Chapter | Next Chapter |